Research Project

The 5D Universe of
3D‑Space & 2D‑Complex Time

Perceptions of the natural world are dramatically changed by examining commonly observed phenomena in higher dimensions. The spacekime theory translates mathematical-physics concepts into data-science analytics where particles and wave-functions become data and inference-functions.

TCIU Technical Details TCIU AI Tutor & Assistant

Have you ever asked…

These fundamental questions drive the Spacekime research. Answers have profound implications on our interpretation of the universe.

What is time and how are time-measurements different from space-locations?

What is an event and how is it characterized?

Why can't we simultaneously measure the position and the momentum of a moving particle with perfect accuracy?

Is it possible that the universe is higher-dimensional, yet we can only perceive a lower-dimensional projection — a silhouette — of an actual holographic universe?

What is a probability distribution? Can we observe the entire distribution or only see finite-size samples?

What is the Kaluza-Klein Theory and why is it important?

What would the universe look like if the 4D space-time we experience is simply a projection of a higher-dimensional space?

What is Heisenberg's uncertainty principle and how is it related to distribution theory, stochastic, and deterministic dynamics?

The classical first and second fundamental laws of probability theory (CLT and LLN) provide asymptotic results about observed sample statistics. Under what conditions may small-samples still lead to reliable scientific inference?

Do ultrahyperbolic PDEs (like the wave equation) have solutions in multiple time dimensions, and if so, what are the dynamics of potential wavefunctions solving such PDEs?

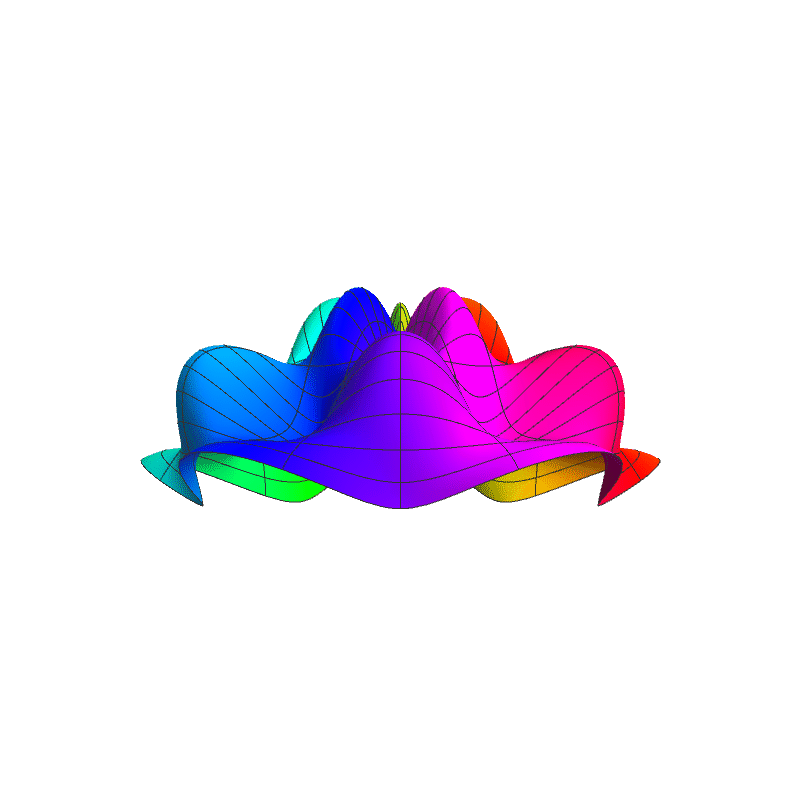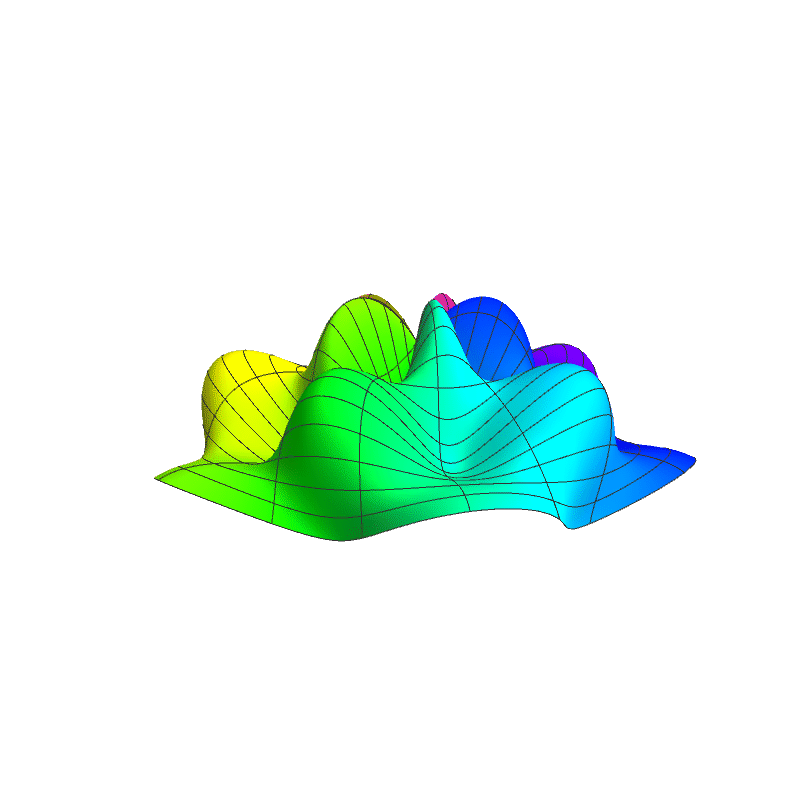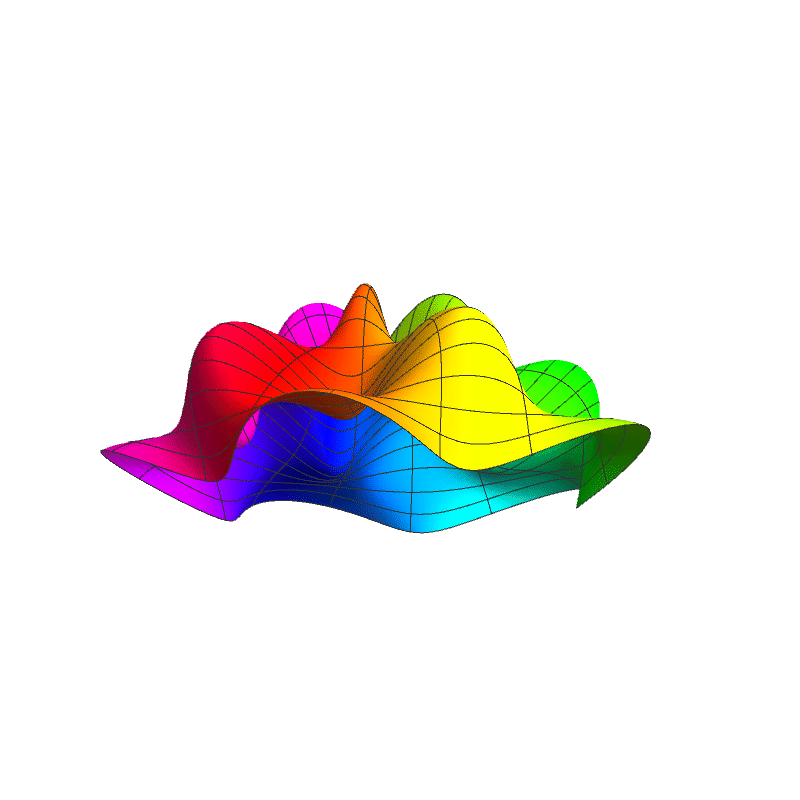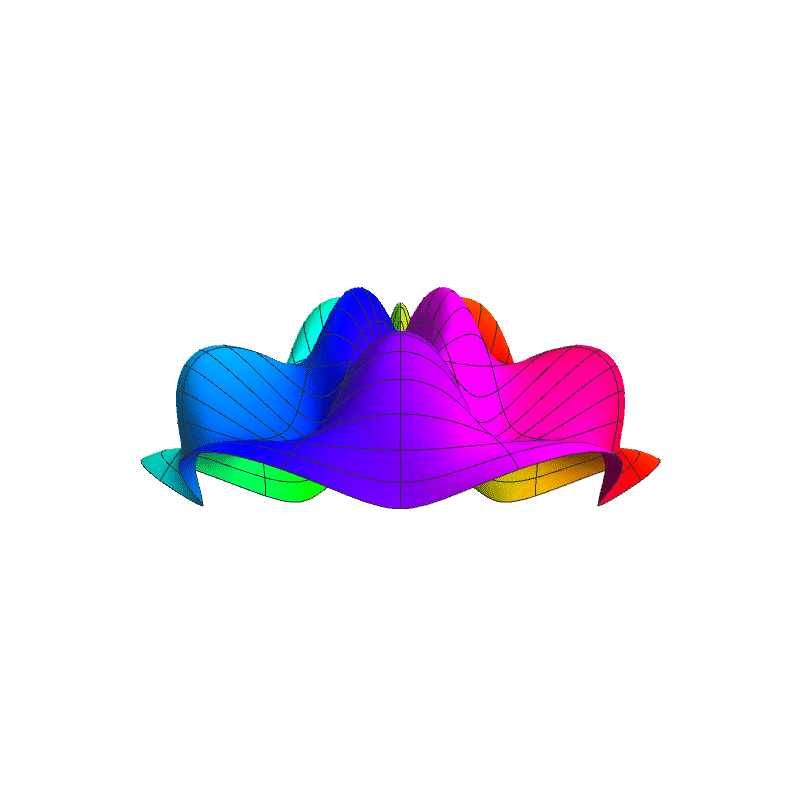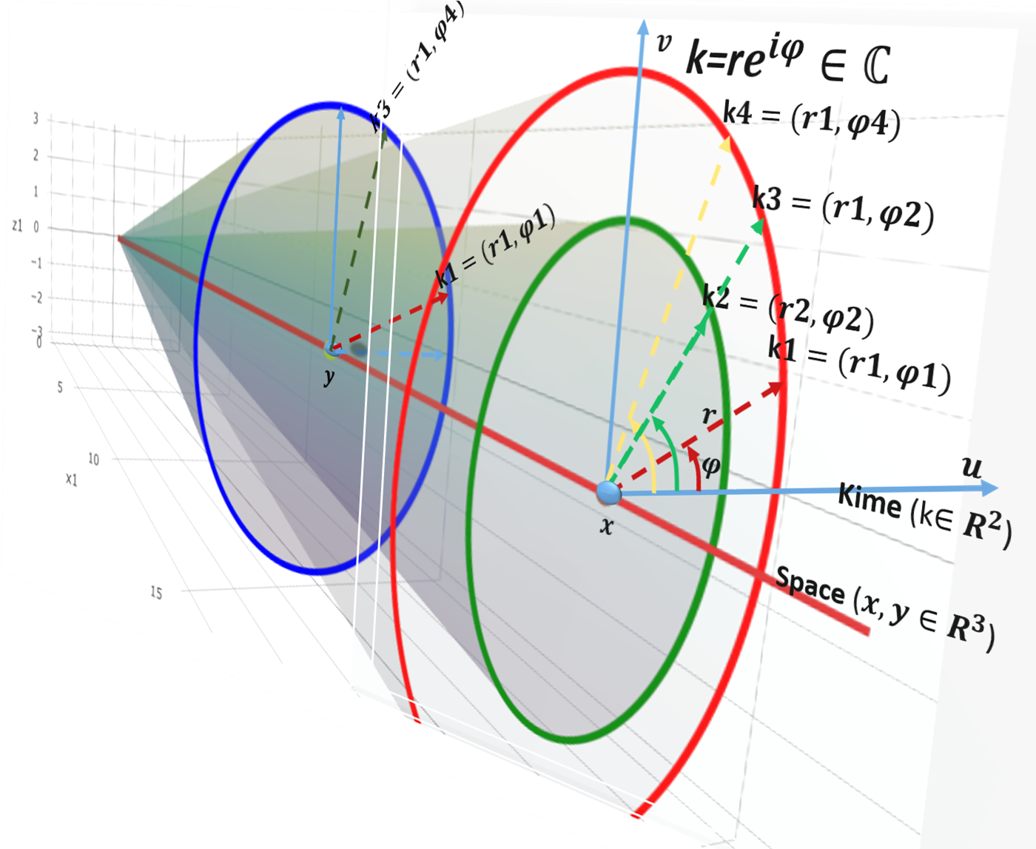
Overview

Extending Time to the Complex Plane

The SOCR group at the University of Michigan is developing a novel theoretical foundation to extend the notion of time to the complex plane. This approach lifts the concept of time from a positive real number representing event ordering to a 2D complex-time (kime) comprising a pair of coordinates — time (t) and phase (φ).

This enables powerful data-driven analytical strategies for large longitudinal data. The 5D spacekime analytics utilize information measures, entropy, KL divergence, PDEs, Dirac's bra-ket operators, and the Fourier transform.

This data science fundamentals research project explores time-complexity and inferential uncertainty in modeling, analyzing, and interpreting large, heterogeneous, multi-source, multi-scale, incomplete, incongruent, and longitudinal data.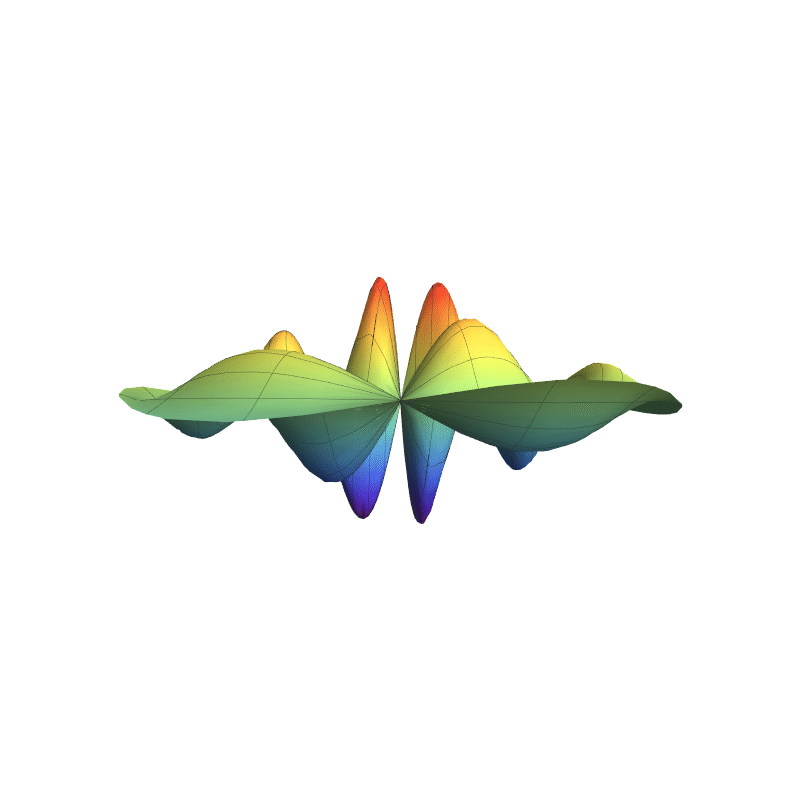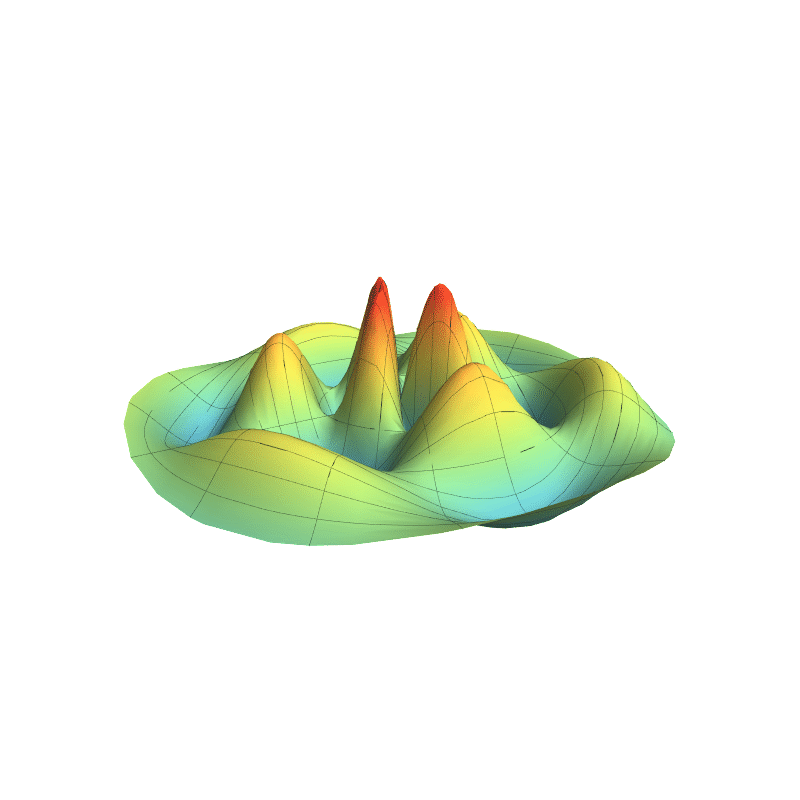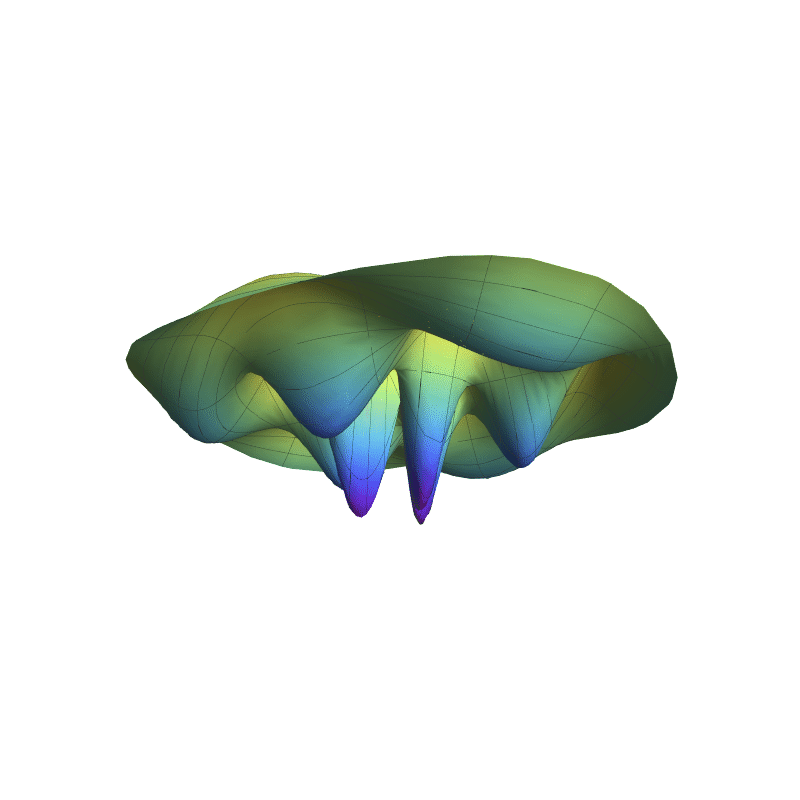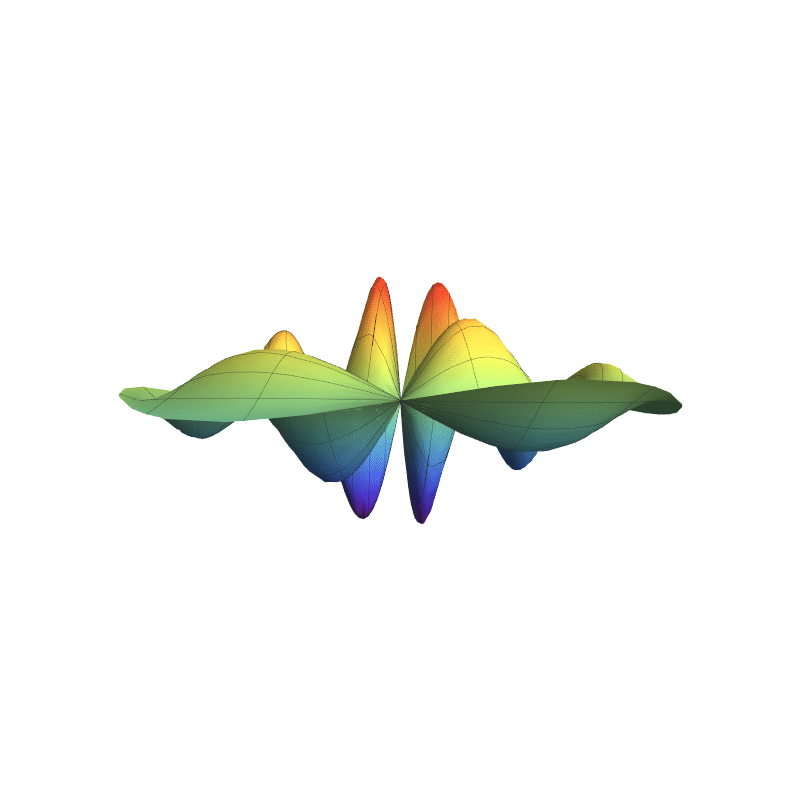

Click to explore an interactive kimesurface. The height represents kime-series intensity, encoded in rainbow color.

Kime-series

From Time-Series Curves to Kimesurfaces

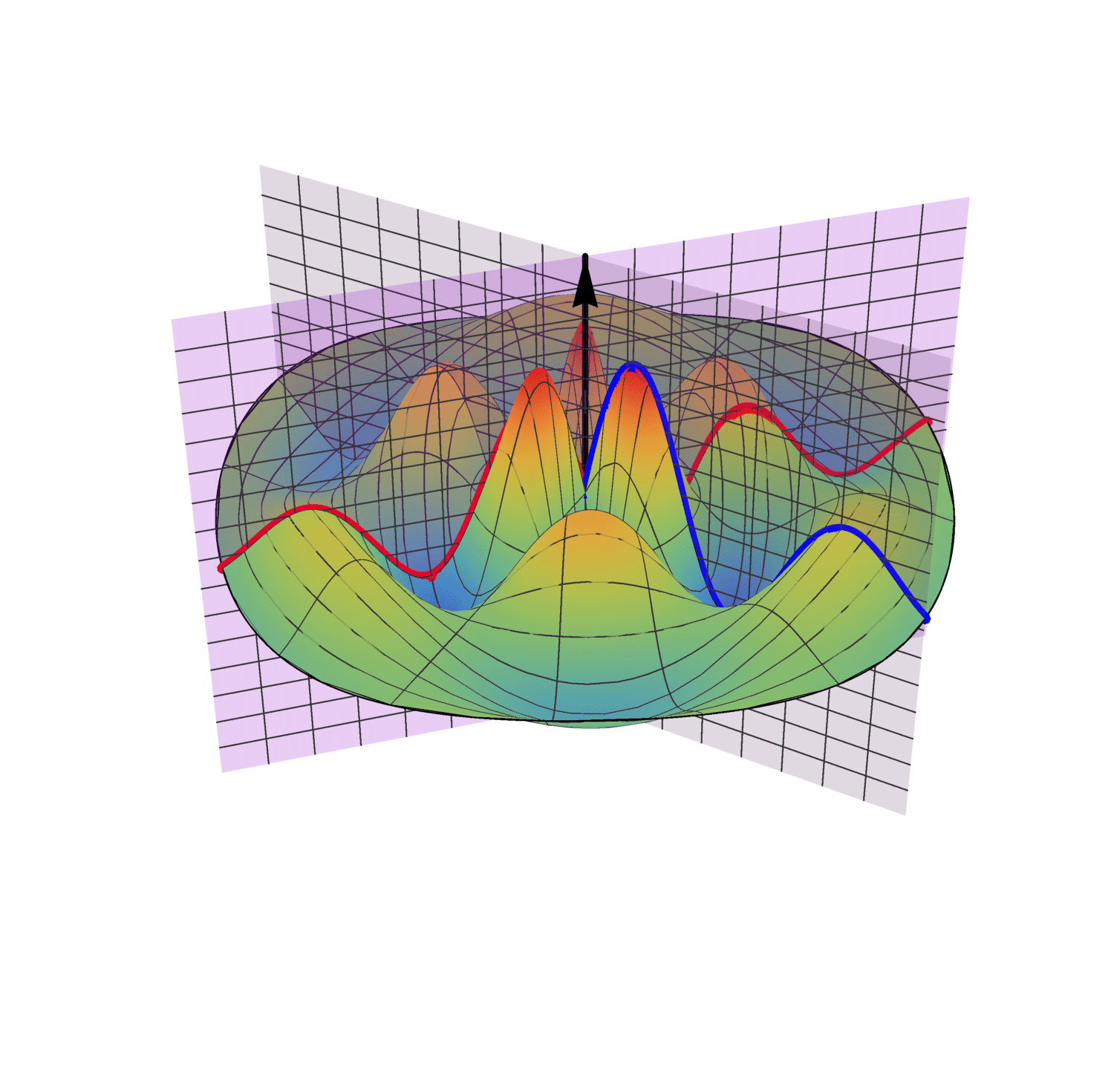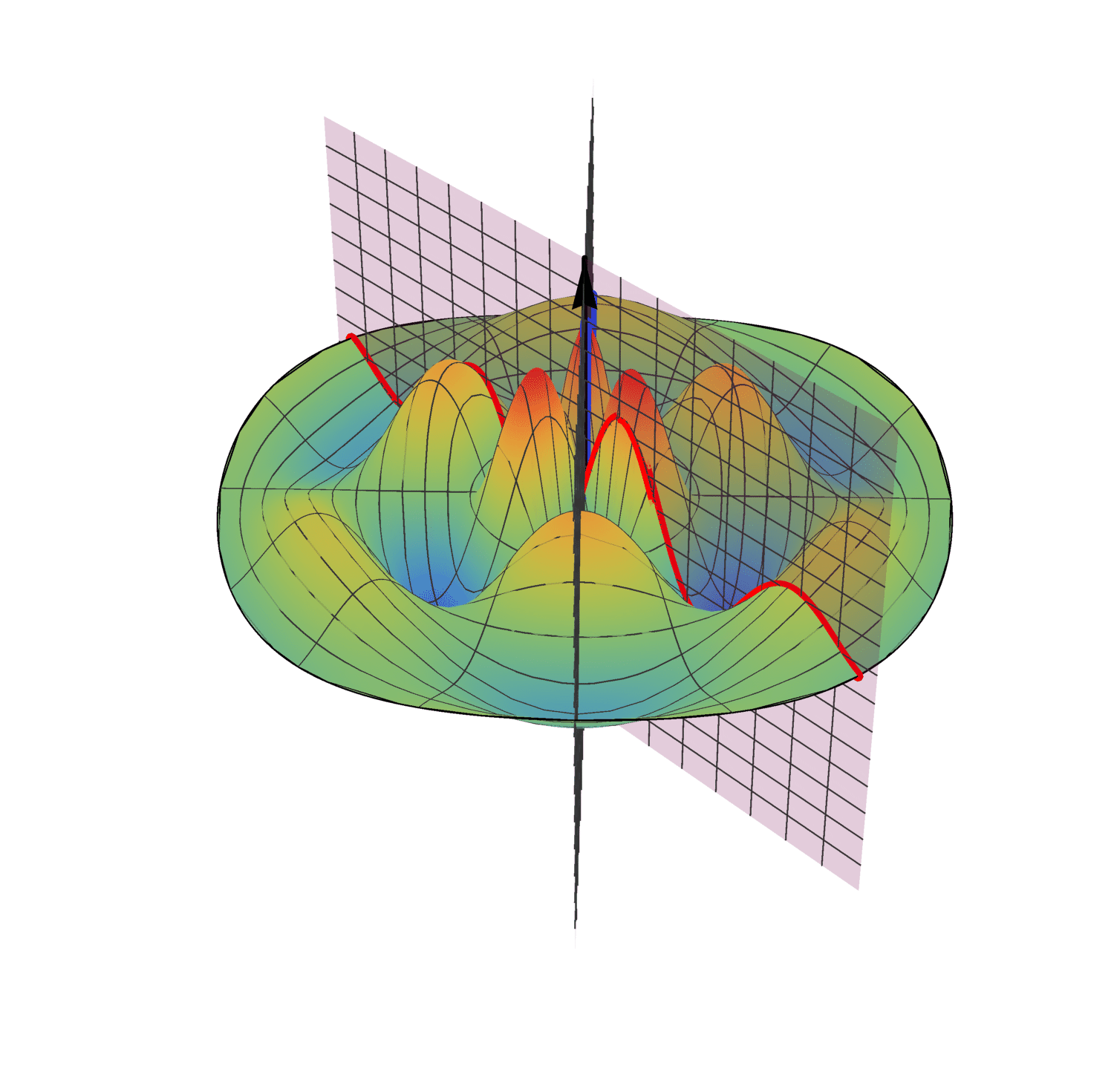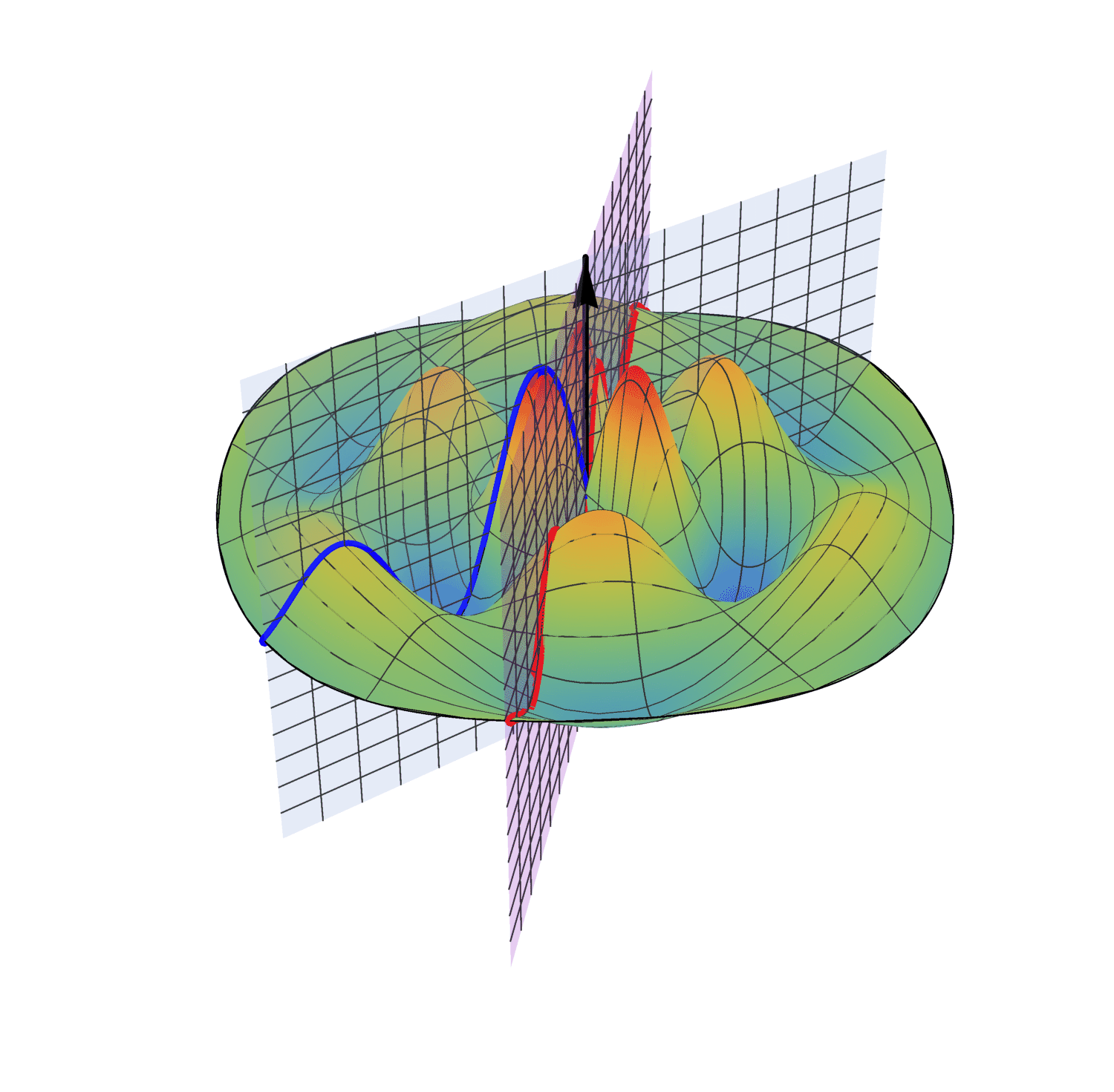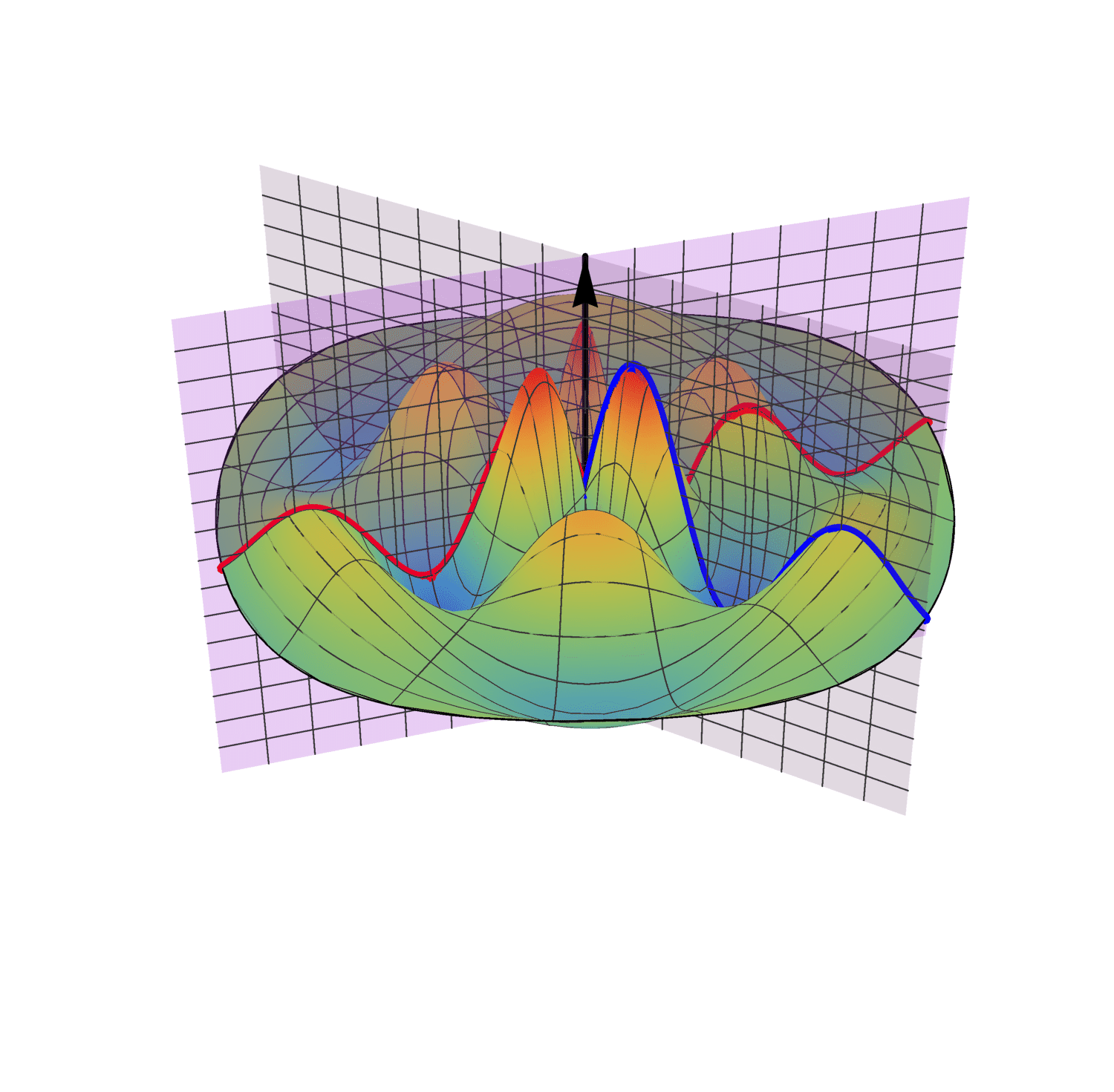
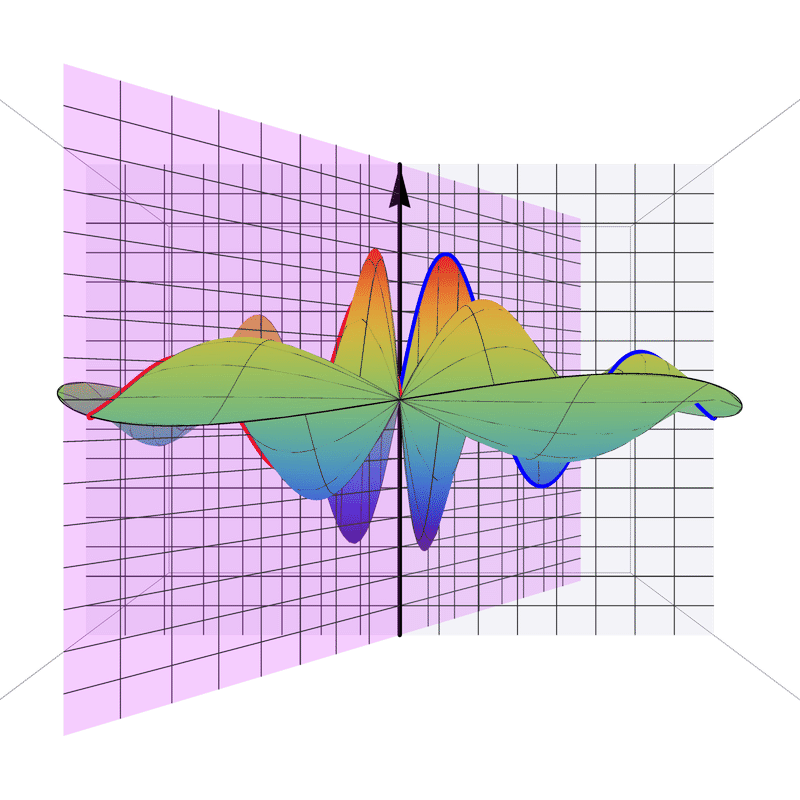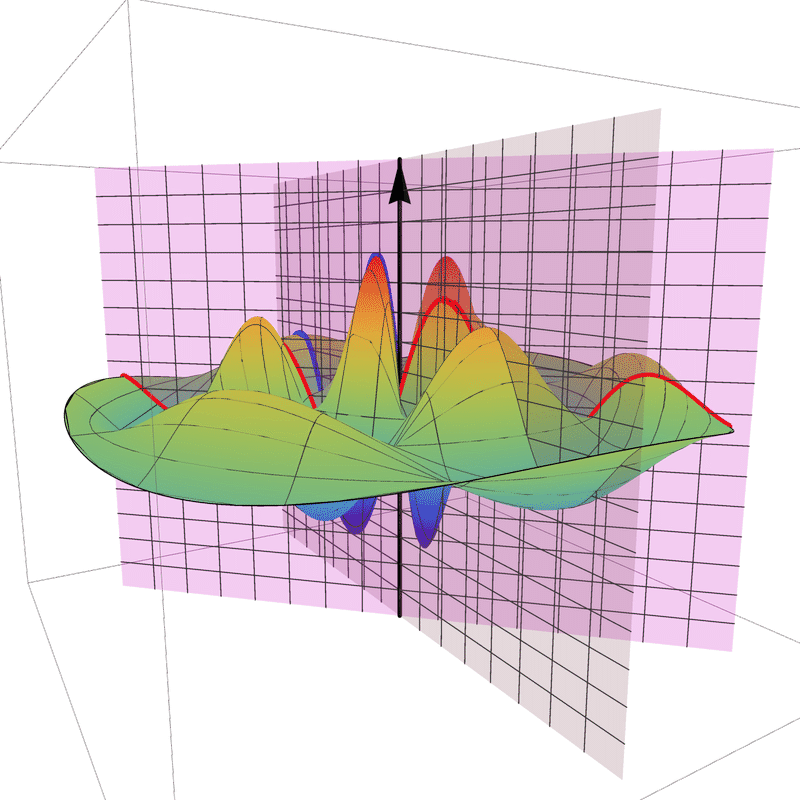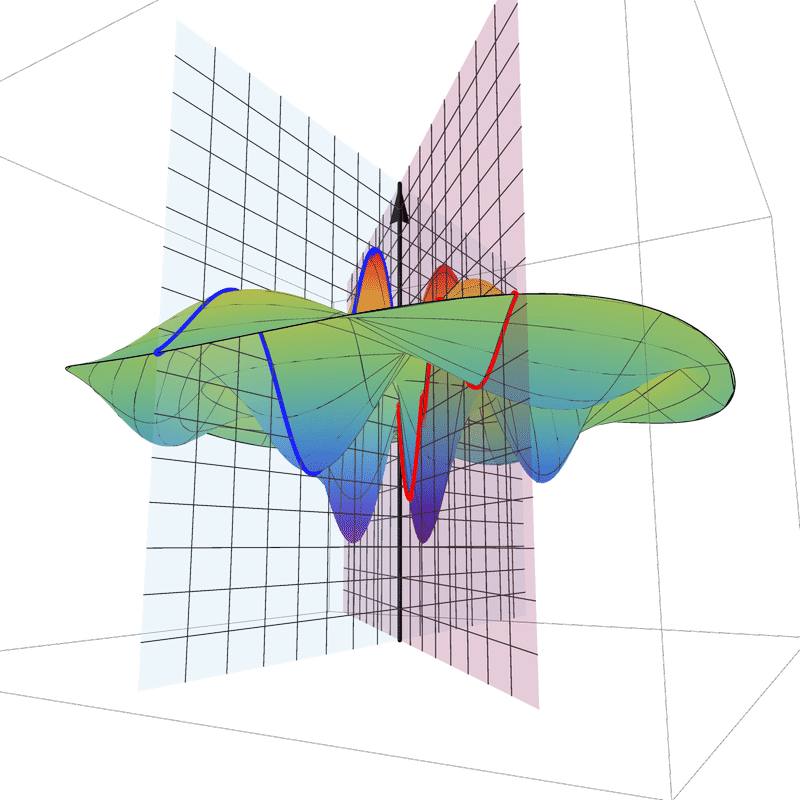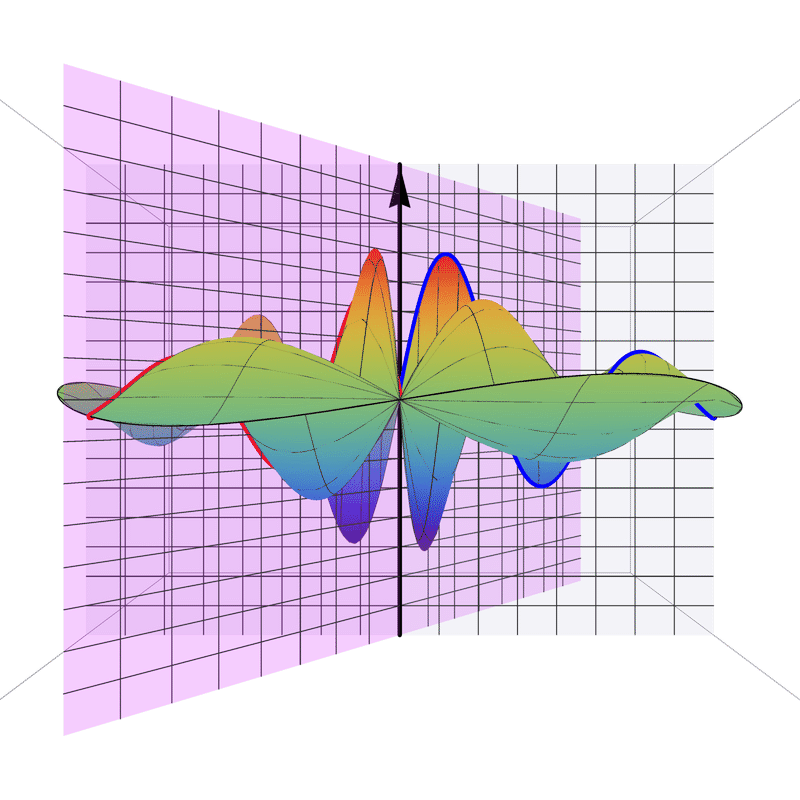
In 4D spacetime, classical time-series are real-valued functions defined over the positive real time domain. In the 5D spacekime manifold, time-series extend to kime-series, represented geometrically as surfaces.

In many disciplines — music, economics, biomedicine, and health sciences — the flow of data is time-dependent. In spacekime, these time-courses are actually complex-time surfaces (kimesurfaces) whose realizations in the lower-dimensional 4D spacetime appear simply as curves over time.

At any given kime — for a pair of arguments kime-magnitude (t) and kime-phase (φ) — the height of the kime-surface represents the intensity of the kime-series. Observable time-series are just intersections of the more general kimesurfaces with 2D leaf foliation manifolds, e.g., planes. The third animation shows an idealized complex-valued, kime-indexed fMRI at one spatial location, where the domain is indexed by kime magnitude (time) and phase (direction), and the amplitude and phase of fMRI intensity are encoded by height (z-axis) and color (RGB).

For a concrete example, imagine a symphony performance in a concert hall. At roughly the same time and spatial location, all attendees receive the same longitudinal input — temporal audio-visual-tactile stimuli. Yet after the performance, all leave with different experiences, distinct impressions, and unique opinions. At each moment, all observers share the same spacetime location, but their differential experiences correspond to random sampling through the kime-phase space (Φ), explaining their uniquely individual encounters. After the performance, communication and stratification of individual experiences lead to a "consensus" capturing the joint experience — kime-averaging of all impressions gives a yardstick measure that can compare, contrast, or calibrate similar performances.

The Spacekime Community Site has a blog tracking some spacekime activities and includes generative AI textual and imaging interpretations of complex time and spacekime.

Deep Dive

About Spacekime

Complex Time (Kime)

Over 100 years ago, the ideas of many polymaths materialized into a unifying notion of an integrated 4D Minkowski space-time. Kaluza and Klein first asked what may be the implications of adding a special tiny fifth dimension. Later the work of Wesson, Bars, and the 5D space-time-matter consortium generalized this idea.

The SOCR team is extending the interpretation of the universe as a 5D space-kime manifold where time is no longer simply a positive unidirectional concept, but a complete field isomorphic to the complex numbers — leading to extensions of time, events, and spacetime metric to their more general counterparts: kime, kevents, and spacekime metric tensor.

This resolves some of the problems of time and enables formulation of time-dependent properties as process characteristics derived using 2D kime. The quantum mechanical notions of particle and wavefunction are extended to datasets and data science analytics.

Spacekime Details

The time-complexity and inferential-uncertainty textbook provides detailed formulation of the spacekime manifold and its applications to data science and longitudinal health analytics.

Spacekime Data Analytics

The lifting of the 4D spacetime into the 5D spacekime manifold has profound implications on the collection, modeling, interpretation, and analytics of all longitudinal information. Two specific implications include:

Reduction of the need for large-samples to estimate specific population characteristics
Improvement of subsequent data analytics performed on spacekime-transformed data

Learn more at www.spacekime.org or by contacting SOCR's Director, Prof. Ivo Dinov.

Spacekime Project Goals

This project aims to answer deep and fundamental questions like:

How to translate centuries of fundamental mathematics and physics ideas into data science?
Can large-sample theory be replaced by small-samples with some prior knowledge?
Is the universe really four-dimensional?
What if there is no arrow of time and we can traverse spacetime in any direction?
Would lifting the spacetime dimension lead to differences in interpretation and improvement of data-driven inference?

Spacekime Publications

See the SOCR Publications Website →

The 5D Universe of 3D‑Space & 2D‑Complex Time