"
#' date: "`r format(Sys.time(), '%B %Y')`"
#' tags: [DSPA, SOCR, MIDAS, Big Data, Predictive Analytics]
#' output:
#' html_document:
#' self_contained: yes
#' theme: spacelab
#' highlight: tango
#' includes:
#' before_body: SOCR_header.html
#' toc: true
#' number_sections: true
#' toc_depth: 2
#' toc_float:
#' collapsed: false
#' smooth_scroll: true
#' code_folding: show
#' ---
#'
#' In this chapter, we will discuss strategies to `import` data and `export` results. Also, we are going to learn the basic tricks we need to know about processing different types of data. Specifically, we will illustrate common `R` data structures and strategies for loading (ingesting) and saving (regurgitating) data. In addition, we will (1) present some basic statistics, e.g., for measuring central tendency (mean, median, mode) or dispersion (variance, quartiles, range), (2) explore simple plots, (3) demonstrate the uniform and normal distributions, (4) contrast numerical and categorical types of variables, (5) present strategies for handling incomplete (missing) data, and (6) show the need for cohort-rebalancing when comparing imbalanced groups of subjects, cases or units.
#'
#' # Saving and Loading R Data Structures
#'
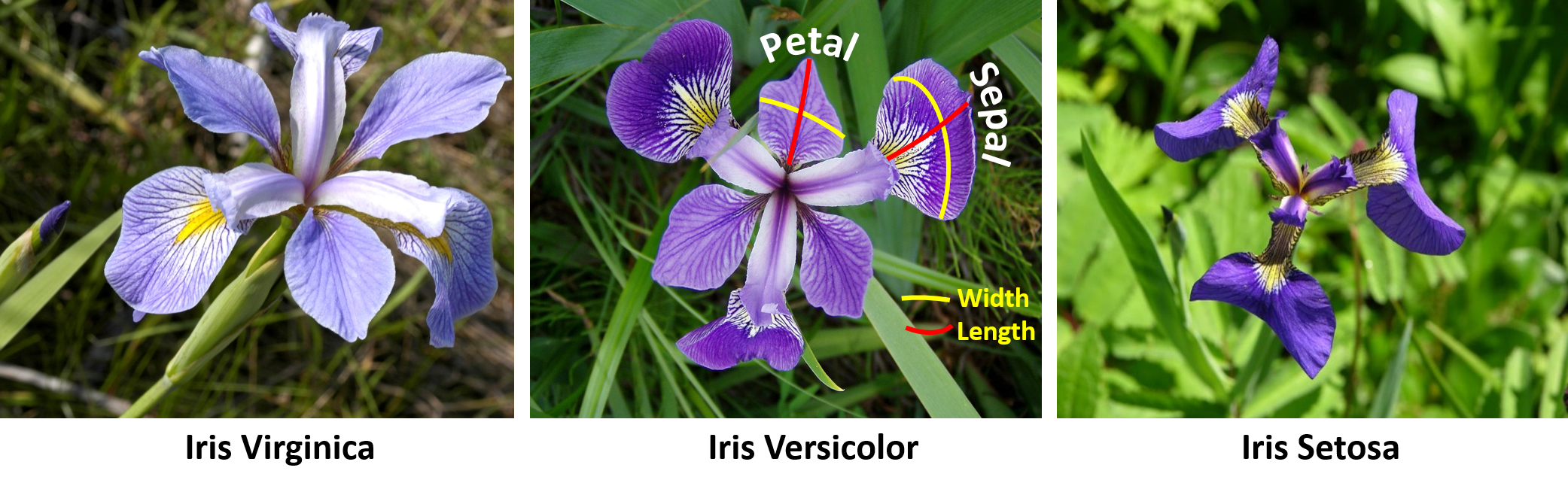
#' Let's start by extracting the Edgar Anderson's Iris Data from the package `datasets`. The [iris dataset](https://en.wikipedia.org/wiki/Iris_flower_data_set) quantifies morphologic shape variations of 50 Iris flowers of three related genera - *Iris setosa*, *Iris virginica* and *Iris versicolor*. Four shape features were measured from each sample - length and the width of the sepals and petals (in centimeters). These data were used by [Ronald Fisher](https://en.wikipedia.org/wiki/Ronald_Fisher) in his [1936 linear discriminant analysis paper](https://doi.org/10.1111%2Fj.1469-1809.1936.tb02137.x).
#'
#'
data()
data(iris)
class(iris)
#'
#' 
#'
#' As an I/O (input/output) demonstration, after we load the `iris` data and examine its class type, we can save it into a file named "myData.RData" and then reload it back into `R`.
#'
#'
save(iris, file="myData.RData")
load("myData.RData")
#'
#'
#' # Importing and Saving Data from CSV Files
#'
#' Importing the data from `"CaseStudy07_WorldDrinkingWater_Data.csv"` from [these case-studies](https://umich.instructure.com/courses/38100/files/folder/Case_Studies) and saving it into the R dataset named "water". The variables in the dataset are as follows:
#'
#' * **Time**: Years (1990, 1995, 2000, 2005, 2010, 2012)
#' * **Demographic**: Country (across the world)
#' * **Residence Area Type**: Urban, rural, or total
#' * **WHO Region**
#' * **Population using improved drinking-water sources**: The percentage of the population using an improved drinking water source.
#' * **Population using improved sanitation facilities**: The percentage of the population using an improved sanitation facility.
#'
#' Generally, the separator of a CSV file is comma. By default, we have option`sep=", "` in the command `read.csv()`. Also, we can use `colnames()` to rename the column variables.
#'
#'
water <- read.csv('https://umich.instructure.com/files/399172/download?download_frd=1', header=T)
water[1:3, ]
colnames(water)<-c("year", "region", "country", "residence_area", "improved_water", "sanitation_facilities")
water[1:3, ]
which.max(water$year);
# rowMeans(water[,5:6])
mean(water[,6], trim=0.08, na.rm=T)
#'
#'
#' This code loads CSV files that already include a header line listing the names of the variables. If we don't have a header in the dataset, we can use the `header = FALSE` option to fix it. R will assign default names to the column variables of the dataset.
#'
#'
Simulation <- read.csv("https://umich.instructure.com/files/354289/download?download_frd=1", header = FALSE)
Simulation[1:3, ]
#'
#'
#' To save a data frame to CSV files, we could use the `write.csv()` function. The option `file = "a/local/file/path"` allow us edit the saved file path.
#'
write.csv(iris, file = "C:/Users/iris.csv")
#'
#'
#' # Importing Data from ZIP and SAV Files
#'
#' This example demonstrates data import from a compressed (ZIP) SPSS (SAV) file. In this case, we utilize DSPA [Case-Study 25: National Ambulatory Medical Care Survey (NAMCS)](https://umich.instructure.com/courses/38100/files/folder/Case_Studies/25_NAMCS_2015).
#'
#'
# install.packages("foreign")
library("foreign")
pathToZip <- tempfile()
download.file("https://umich.instructure.com/files/8111611/download?download_frd=1", pathToZip, mode = "wb")
dataset <- read.spss(unzip(pathToZip, files = "namcs2015-spss.sav", list = F, overwrite = TRUE), to.data.frame=TRUE)
dim(dataset)
## [1] 28332 1096
# str(dataset)
# View(dataset)
unlink(pathToZip)
#'
#'
#' # Exploring the Structure of Data
#'
#' We can use the command `str()` to explore the structure of a dataset.
#'
str(water)
#'
#'
#' We can see that this `World Drinking Water` dataset has 3331 observations and 6 variables. The output also includes the class of each variable and first few elements in the variable.
#'
#' # Exploring Numeric Variables
#'
#' Summary statistics for numeric variables in the dataset could be accessed by using the command `summary()`.
#'
#'
library(plotly)
summary(water$year)
summary(water[c("improved_water", "sanitation_facilities")])
plot(density(water$improved_water,na.rm = T)) # no need to be continuous, we can still get intuition about the variable distribution
fit <- density(as.numeric(water$improved_water),na.rm = T)
plot_ly(x = fit$x, y = fit$y, type = "scatter", mode = "lines",
fill = "tozeroy", name = "Density") %>%
layout(title='Density of (%) Improved Water Quality',
xaxis = list (title = 'Percent'), yaxis = list (title = 'Density'))
#'
#'
#' The six summary statistics and `NA`'s (missing data) are reported in the output.
#'
#' # Measuring the Central Tendency - mean, median, mode
#'
#' **Mean** and **median** are two frequent measurements of the central tendency. Mean is "the sum of all values divided by the number of values". Median is the number in the middle of an ordered list of values. In R, `mean()` and `median()` functions can provide us with these two measurements.
#'
vec1<-c(40, 56, 99)
mean(vec1)
mean(c(40, 56, 99))
median(vec1)
median(c(40, 56, 99))
# install.packages("psych");
library("psych")
geometric.mean(vec1, na.rm=TRUE)
#'
#'
#' The **mode** is the value that occurs most often in the dataset. It is often used in categorical data, where mean and median are inappropriate measurements.
#'
#' We can have one or more modes. In the [water dataset](https://umich.instructure.com/files/399172/download?download_frd=1), we have "Europe" and "Urban" as the modes for region and residence area respectively. These two variables are unimodal, which has a single mode. For the year variable, we have two modes 2000 and 2005. Both of the categories have 570 counts. The year variable is an example of a bimodal. We also have multimodal that has two or more modes in the data.
#'
#' Mode is one of the measures for the central tendency. The best way to use it is to comparing the counts of the mode to other values. This help us to judge whether one or several categories dominates all others in the data. After that, we are able to analyze the story behind these common ones.
#'
#' In numeric datasets, we could think mode as the highest bin in the histogram, since it is unlikely to have many repeated measurements for continuous variables. In this way, we can also examine if the numeric data is multimodal.
#'
#' [More information about measures of centrality is available here](https://wiki.socr.umich.edu/index.php/AP_Statistics_Curriculum_2007_EDA_Center).
#'
#' # Measuring Spread - quartiles and the five-number summary
#'
#' The five-number summary describes the spread of a dataset. They are:
#'
#' * Minimum (`Min.`), representing the smallest value in the data
#' * First quantile/Q1 (`1st Qu.`), representing the $25^{th}$ percentile, which splits off the lowest 25% of data from the highest 75%
#' * Median/Q2 (`Median`), representing the $50^{th}$ percentile, which splits off the lowest 50% of data from the top 50%
#' * Third quantile/Q3 (`3rd Qu.`), representing the $75^{th}$ percentile, which splits off the lowest 75% of data from the top 25%
#' * Maximum (`Max.`), representing the largest value in the data.
#'
#' `Min` and `Max` can be obtained by using `min()` and `max()` respectively.
#'
#' The difference between maximum and minimum is known as range. In R, `range()` function give us both the minimum and maximum. An combination of `range()` and `diff()` could do the trick of getting the actual range value.
#'
#'
range(water$year)
diff(range(water$year))
#'
#'
#' Q1 and Q3 are the 25th and 75th percentiles of the data. Median (Q2) is right in the middle of Q1 and Q3. The difference between Q3 and Q1 is called the interquartile range (IQR). Within the IQR lies half of our data that has no extreme values.
#'
#' In R, we use the `IQR()` to calculate the interquartile range. If we use `IQR()` for a data with `NA`'s, the `NA`'s are ignored by the function while using the option `na.rm=TRUE`.
#'
#'
IQR(water$year)
summary(water$improved_water)
IQR(water$improved_water, na.rm = T)
#'
#'
#' Just like the command `summary()` that we have talked about earlier in this chapter. A similar function `quantile()` could be used to obtain the five-number summary.
#'
#'
quantile(water$improved_water, na.rm = T)
#'
#'
#' We can also calculate specific percentiles in the data. For example, if we want the 20th and 60th percentiles, we can do the following.
#'
#'
quantile(water$improved_water, probs = c(0.2, 0.6), na.rm = T)
#'
#'
#' When we include the `seq()` function, generating percentiles of evenly-spaced values is available.
#'
#'
quantile(water$improved_water, seq(from=0, to=1, by=0.2), na.rm = T)
#'
#'
#' Let's re-examine the five-number summary for the `improved_water` variable. When we ignore the `NA`'s, the difference between minimum and Q1 is 74 while the difference between Q3 and maximum is only 1. The interquartile range is 22%. Combining these facts, the first quarter is more widely spread than the middle 50 percent of values. The last quarter is the most condensed one that has only two percentages 99% and 100%. Also, we can notice that the mean is smaller than the median. The mean is more sensitive to the extreme values than the median. We have a very small minimum that makes the range of first quantile very large. This extreme value impacts the mean less than the median.
#'
#' # Visualizing Numeric Variables - boxplots
#'
#' We can visualize the five-number summary by a boxplot (box-and-whiskers plot). With the `boxplot()` function we can manage the title (`main=""`) and labels for x (`xlab=""`) and y (`ylab=""`) axis.
#'
#'
#boxplot(water$improved_water, main="Boxplot for Percent improved_water", ylab="Percentage")
plot_ly(y = ~water$improved_water, type = "box", name="improved water qual") %>%
add_trace(y = ~water$sanitation_facilities, name ="sanitation") %>%
layout(title='Boxplots of Improved Water Quality and Sanitation Facilities',
yaxis = list (title = 'Percent'))
#'
#'
#' In the boxplot we have five horizontal lines each represents the corresponding value in the five-number summary. The box in the middle represents the middle 50 percent of values. The bold line in the box is the median. Mean value is not illustrated on the graph.
#'
#' Boxplots only allow the two ends to extend to a minimum or maximum of 1.5 times the IQR. Therefore, any value that falls outside of the $3\times IQR$ range will be represented as circles or dots. They are considered outliers. We can see that there are a lot of outliers with small values on the low ends of the graph.
#'
#' # Visualizing Numeric Variables - histograms
#'
#' Histogram is another way to show the spread of a numeric variable, see [Chapter 3](https://www.socr.umich.edu/people/dinov/courses/DSPA_notes/03_DataVisualization.html) for additional information). It uses predetermined number of bins as containers for values to divide the original data. The height of the bins indicates frequency.
#'
#'
# hist(water$improved_water, main = "Histogram of Percent improved_water", xlab="Percentage")
# hist(water$sanitation_facilities, main = "Histogram of Percent sanitation_facilities", xlab = "Percentage")
plot_ly(x = ~water$improved_water, type = "histogram", name="improved_water") %>%
add_trace(x = ~water$sanitation_facilities, type = "histogram", name="sanitation_facilities") %>%
layout(bargap=0.1, title='Histograms', legend = list(orientation = 'h'),
xaxis = list(title = 'Percent'), yaxis = list (title = 'Frequency'))
#'
#'
#' We could see that the shape of two graphs are somewhat similar. They are both left skewed patterns ($mean \lt median$). Other common skew patterns are shown in the following picture.
#'
#'
N <- 10000
x <- rnbinom(N, 5, 0.1)
# hist(x,
# xlim=c(min(x), max(x)), probability=T, nclass=max(x)-min(x)+1,
# col='lightblue', xlab=' ', ylab=' ', axes=F,
# main='Right Skewed')
# lines(density(x, bw=1), col='red', lwd=3)
fit <- density(x)
plot_ly(x = x, type = "histogram", name = "Data Histogram") %>%
add_trace(x = fit$x, y = fit$y, type = "scatter", mode = "lines", opacity=0.3,
fill = "tozeroy", yaxis = "y2", name = "Density (rnbinom(N, 5, 0.1))") %>%
layout(title='Right Skewed Process', yaxis2 = list(overlaying = "y", side = "right"),
legend = list(orientation = 'h'))
N <- 10000
x <- rnorm(N, 15, 3.7)
# hist(x,
# xlim=c(min(x), max(x)), probability=T, nclass=max(x)-min(x)+1,
# col='lightblue', xlab=' ', ylab=' ', axes=F,
# main='Right Skewed')
# lines(density(x, bw=1), col='red', lwd=3)
fit <- density(x)
plot_ly(x = x, type = "histogram", name = "Data Histogram") %>%
add_trace(x = fit$x, y = fit$y, type = "scatter", mode = "lines", opacity=0.3,
fill = "tozeroy", yaxis = "y2", name = "Density (rnorm(N, 15, 3.7))") %>%
layout(title='Symmetric Process', yaxis2 = list(overlaying = "y", side = "right"),
legend = list(orientation = 'h'))
#'
#'
#' You can learn more about [Probability Distributions in the SOCR EBook](https://wiki.socr.umich.edu/index.php/EBook#Chapter_IV:_Probability_Distributions) and see the density plots of over 80 different probability distributions using the [SOCR Java Distribution Calculators](https://socr.umich.edu/html/dist/) or the [Distributome HTML5 Distribution Calculators](http://www.distributome.org/V3/calc/index.html).
#'
#' For each probability distribution defined in R, there are four functions that provide the density (e.g., `dnorm`), the cumulative probability (e.g., `pnorm`), the inverse cumulative distribution (quantile) function (e.g., `qnorm`), and the random sampling (simulation) function (e.g., `rnorm`). The plots below show the *standard normal* density, cumulative probability and the quantile functions. As the density is very small outside of the interval $(-4,4)$, the plots are restricted to this domain.
#'
#'
z<-seq(-4, 4, 0.1) # points from -4 to 4 in 0.1 steps
q<-seq(0.001, 0.999, 0.001) # probability quantile values from 0.1% to 99.9% in 0.1% steps
dStandardNormal <- data.frame(Z=z, Density=dnorm(z, mean=0, sd=1), Distribution=pnorm(z, mean=0, sd=1))
qStandardNormal <- data.frame(Q=q, Quantile=qnorm(q, mean=0, sd=1))
head(dStandardNormal)
# plot(z, dStandardNormal$Density, main="Normal Density Curve", type = "l", xlab = "critical values", ylab="density", lwd=4, col="blue")
# polygon(z, dStandardNormal$Density, col="red", border="blue")
# plot(z, dStandardNormal$Distribution, main="Normal Distribution", type = "l", xlab = "critical values", ylab="Cumulative Distribution", lwd=4, col="blue")
# plot(q, qStandardNormal$Quantile, main="Normal Quantile Function (Inverse CDF)", type = "l", xlab = "p-values", ylab="Critical Values", lwd=4, col="blue")
plot_ly(x = z, y= dStandardNormal$Density, name = "Normal Density Curve",
mode = 'lines') %>%
layout(title='Normal Density Curve',
xaxis = list(title = 'critical values'),
yaxis = list(title ="Density"),
legend = list(orientation = 'h'))
plot_ly(x = z, y= dStandardNormal$Distribution,
name = "Normal Density Curve", mode = 'lines') %>%
layout(title='Normal Distribution',
xaxis = list(title = 'critical values'),
yaxis = list(title ="Cumulative Distribution"),
legend = list(orientation = 'h'))
plot_ly(x = q, y= qStandardNormal$Quantile,
name = "Normal Quantile Function (Inverse CDF)", mode = 'lines') %>%
layout(title='Normal Distribution',
xaxis = list(title = 'probability values'),
yaxis = list(title ="Critical Values"),
legend = list(orientation = 'h'))
#'
#'
#' # Understanding Numeric Data - uniform and normal distributions
#'
#' If the data follows a *uniform distribution*, then all values are equally likely to occur. The histogram for a uniformly distributed data would have equal heights for each bin like the following graph.
#'
#'
x<-runif(1000, 1, 50)
# hist(x, col='lightblue', main="Uniform Distribution", probability = T, xlab="", ylab="Density", axes=F)
# abline(h=0.02, col='red', lwd=3)
plot_ly(x = ~x, type = "histogram", histnorm = "probability", name="proportion", showlegend = F) %>%
add_lines(x=~x, y=~0.038, type = 'scatter', mode = 'lines') %>%
layout(bargap=0.1, title='Uniform(0, 50) Histogram', yaxis = list(title ="probability"))
#'
#'
#' Often, but not always, real world processes may appear as normally distributed data. A *normal distribution* would have a higher frequency for middle values and lower frequency for more extreme values. It has a symmetric and bell-curved shape just like the following diagram generated by R. Many parametric-based statistical approaches assume normality of the data. In cases where this parametric assumption is violated, variable transformations or distribution-free tests may be more appropriate.
#'
#'
N<- 1000
norm <- rnorm(N, 0, 1)
# hist(x, probability=T,
# col='lightblue', xlab=' ', ylab=' ', axes=F,
# main='Normal Distribution')
# lines(density(x, bw=0.4), col='red', lwd=3)
normDensity <- density(norm, bw=0.5)
dens <- data.frame(x = normDensity$x, y = normDensity$y)
miny <- 0
maxy <- max(dens$y)
plot_ly(dens) %>%
add_histogram(x = norm, name="Normal Histogram") %>%
add_lines(data = dens, x = ~x, y = ~y, yaxis = "y2",
line = list(width = 3), name="N(0,1)") %>%
layout(bargap=0.1, yaxis2 = list(overlaying = "y", side = "right",
range = c(miny, maxy), showgrid = F, zeroline = F),
legend = list(orientation = 'h'), title="Normal(0,1)")
#'
#'
#' # Measuring Spread - variance and standard deviation
#'
#' Distribution is a great way to characterize data using only a few parameters. For example, normal distribution can be defined by only two parameters center and spread or statistically mean and standard deviation.
#'
#' The way to get mean value is to divide the sum of the data values by the number of values. So, we have the following formula.
#'
#' $$Mean(X)=\mu=\frac{1}{n}\sum_{i=1}^{n} x_i$$
#'
#' The standard deviation is the square root of the variance. Variance is the average sum of square.
#'
#' $$Var(X)=\sigma^2=\frac{1}{n-1}\sum^{n}_{i=1} (x_i-\mu)^2$$
#' $$StdDev(X)=\sigma=\sqrt{Var(X)}$$
#'
#' Since the water dataset is non-normal, we use a new dataset about the demographics of baseball players to illustrate normal distribution properties. The `"01_data.txt"` in our class file has following variables:
#'
#' * Name
#' * Team
#' * Position
#' * Height
#' * Weight
#' * Age
#'
#' We check the histogram for approximate normality first.
#'
#'
baseball<-read.table("https://umich.instructure.com/files/330381/download?download_frd=1", header=T)
# hist(baseball$Weight, main = "Histogram for Baseball Player's Weight", xlab="weight")
# hist(baseball$Height, main = "Histogram for Baseball Player's Height", xlab="height")
plot_ly(x = ~baseball$Weight, type = "histogram", name="Baseball Weight", showlegend = F) %>%
layout(bargap=0.1, title='Baseball Weight')
plot_ly(x = ~baseball$Height, type = "histogram", name="Baseball Height", showlegend = F) %>%
layout(bargap=0.1, title='Baseball Height')
#'
#'
#' This plot allows us to visually inspect the normality of the players height and weight. We could also obtain mean and standard deviation of the weight and height variables.
#'
mean(baseball$Weight)
mean(baseball$Height)
var(baseball$Weight)
sd(baseball$Weight)
var(baseball$Height)
sd(baseball$Height)
#'
#'
#' Larger standard deviation, or variance, suggest the data is more spread out from the mean. Therefore, the weight variable is more spread than the height variable.
#'
#' Given the first two moments (mean and standard deviation), we can easily estimate how extreme a specific value is. Assuming we have a normal distribution, the values follow a $68-95-99.7$ rule. This means 68% of the data lies within the interval $[\mu-\sigma, \mu+\sigma]$;95% of the data lies within the interval $[\mu-2*\sigma, \mu+2*\sigma]$ and 99.7% of the data lies within the interval $[\mu-3*\sigma, \mu+3*\sigma]$. The following graph plotted by R illustrates the $68-95-99.7$ rule.
#'
#'
x <- rnorm(N, 0, 1)
# hist(x, probability=T,
# col='lightblue', xlab=' ', ylab=' ', axes = F,
# main='68-95-99.7 Rule')
# lines(density(x, bw=0.4), col='red', lwd=3)
# axis(1, at=c(-3, -2, -1, 0, 1, 2, 3), labels = expression(mu-3*sigma, mu-2*sigma, mu-sigma, mu, mu+sigma, mu+2*sigma, mu+3*sigma))
# abline(v=-1, lwd=3, lty=2)
# abline(v=1, lwd=3, lty=2)
# abline(v=-2, lwd=3, lty=2)
# abline(v=2, lwd=3, lty=2)
# abline(v=-3, lwd=3, lty=2)
# abline(v=3, lwd=3, lty=2)
# text(0, 0.2, "68%")
# segments(-1, 0.2, -0.3, 0.2, col = 'red', lwd=2)
# segments(1, 0.2, 0.3, 0.2, col = 'red', lwd=2)
# text(0, 0.15, "95%")
# segments(-2, 0.15, -0.3, 0.15, col = 'red', lwd=2)
# segments(2, 0.15, 0.3, 0.15, col = 'red', lwd=2)
# text(0, 0.1, "99.7%")
# segments(-3, 0.1, -0.3, 0.1, col = 'red', lwd=2)
# segments(3, 0.1, 0.3, 0.1, col = 'red', lwd=2)
xLabels <- c("μ-3σ","μ-2σ", "μ-σ", "μ", "μ+σ", "μ+2σ", "μ+3σ")
labelColors <- c("green", "red", "orange", "black", "orange", "red", "green")
xLocation <- c(-3, -2, -1, 0, 1, 2, 3)
yLocation <- -0.2
data <- data.frame(xLabels, xLocation, yLocation)
plot_ly(dens) %>%
add_histogram(x = norm, name="Normal Histogram", name="") %>%
add_lines(data = dens, x = ~x, y = ~y+0.055, yaxis = "y2",
line = list(width = 3), name="N(0,1)") %>%
add_annotations(x = ~xLocation, y = ~yLocation, type = 'scatter', ax = 20, ay = 40,
mode = 'text', text = ~xLabels, textposition = 'middle right',
textfont = list(color = labelColors, size = 16)) %>%
add_segments(x=-3, xend=-3, y=0, yend=100, name="99.7%", line=list(dash="dash", color="green")) %>%
add_segments(x=-2, xend=-2, y=0, yend=90, name="95%", line=list(dash="dash", color="red")) %>%
add_segments(x=-1, xend=-1, y=0, yend=80, name="68%", line=list(dash="dash", color="orange")) %>%
add_segments(x=1, xend=1, y=0, yend=80, name="68%", line = list(dash = "dash", color="orange")) %>%
add_segments(x=2, xend=2, y=0, yend=90, name="95%", line=list(dash="dash", color="red")) %>%
add_segments(x=3, xend=3, y=0, yend=100, name="99.7%", line=list(dash="dash", color="green")) %>%
add_segments(x=-3, xend=3, y=100, yend=100, name="99.7%", line=list(dash="dash", color="green")) %>%
add_segments(x=-2, xend=2, y=90, yend=90, name="95%", line=list(dash="dash", color="red")) %>%
add_segments(x=-1, xend=1, y=80, yend=80, name="68%", line=list(dash="dash", color="orange")) %>%
layout(bargap=0.1, xaxis=list(name=""), yaxis=list(name=""),
yaxis2 = list(overlaying = "y", side = "right",
range = c(miny, maxy+0.2), showgrid = F, zeroline = F),
legend = list(orientation = 'h'), title="Normal 68-95-99.7% Rule")
#'
#'
#' Applying the 68-95-99.7 rule to our baseball weight variable, we know that 68% of our players weighted between 180.7168 pounds and 222.7164 pounds; 95% of the players weighted between 159.7170 pounds and 243.7162 pounds; And 99.7% of the players weighted between 138.7172 pounds and 264.7160 pounds.
#'
#' # Exploring Categorical Variables
#'
#' Back to our water dataset, we can treat the year variable as categorical rather than a numeric variable. Since the year variable only have six distinctive values, it is rational to treat it as a categorical variable where each value is a category that could apply to multiple WHO regions. Moreover, region and residence area variables are also categorical.
#'
#' Different from numeric variables, the categorical variables are better examined by tables rather than summary statistics. One-way table represents a single categorical variable. It gives us the counts of different categories. `table()` function can create one-way tables for our water dataset:
#'
#'
water <- read.csv('https://umich.instructure.com/files/399172/download?download_frd=1', header=T)
colnames(water)<-c("year", "region", "country", "residence_area", "improved_water", "sanitation_facilities")
table(water$year)
table(water$region)
table(water$residence_area)
#'
#'
#' Given that we have a total of 3331 observations, the WHO region table tells us that about 27% (910/3331) of the areas examined in the study are in Europe.
#'
#' R can directly give us table proportions when using the `prop.table()` function. The proportion values can be transformed into percentage form and edit number of digits.
#'
#'
year_table<-table(water$year)
prop.table(year_table)
year_pct<-prop.table(year_table)*100
round(year_pct, digits=1)
#'
#'
#' # Exploring Relationships Between Variables
#'
#' So far the methods and statistics that we have go through are at univariate level. Sometimes we want to examine the relationship between two or multiple variables. For example, did the percentage of population that uses improved drinking-water sources increase over time? To address these problems we need to look at bivariate or multivariate relationships.
#'
#' **Visualizing Relationships - scatterplots**
#'
#' Let's look at bivariate case first. A scatterplot is a good way to visualize bivariate relationships. We have x axis and y axis each representing one of the variables. Each observation is illustrated on the graph by a dot. If the graph shows a clear pattern rather a group of messy dots or a horizontal line, the two variables may correlated with each other.
#'
#' In R we can use `plot()` function to create scatterplots. We have to define the variables for x-axis and y-axis. The labels in the graph are editable.
#'
#'
# plot.window(c(400,1000), c(500,1000))
# plot(x=water$year, y=water$improved_water,
# main= "Scatterplot of Year vs. Improved_water",
# xlab= "Year",
# ylab= "Percent of Population Using Improved Water")
plot_ly(x = ~water$sanitation_facilities, y = ~water$improved_water, type = "scatter",
mode = "markers") %>%
layout(title='Scatterplot: Improved Water Quality vs. Sanitation Facilities',
xaxis = list (title = 'Water Quality'), yaxis = list (title = 'Sanitation'))
#'
#'
#' We can see from the scatterplot that there is an increasing pattern. In later years, the percentages are more centered around one hundred. Especially, in 2012, not of the regions had less than 20% of people using improved water sources while there used to be some regions that have such low percentages in the early years.
#'
#' **Examining Relationships - two-way cross-tabulations**
#'
#' Scatterplot is a useful tool to examine the relationship between two variables where at least one of them is numeric. When both variables are nominal, two-way cross-tabulation would be a better choice (also named as crosstab or contingency table).
#'
#' The function `CrossTable()` is available in R under the package `gmodels`. Let's install it first.
#'
#'
#install.packages("gmodels", repos = "http://cran.us.r-project.org")
library(gmodels)
#'
#'
#' We are interested in investigating the relationship between WHO region and residence area type in the water study. We might want to know if there is a difference in terms of residence area type between the African WHO region and all other WHO regions.
#'
#' To address this problem we need to create an indicator variable for African WHO region first.
#'
#'
water$africa<-water$region=="Africa"
#'
#'
#' Let's revisit the `table()` function to see how many WHO regions are in Africa.
#'
#'
table(water$africa)
#'
#'
#' Now, let's create a two-way cross-tabulation using `CrossTable()`.
#'
#'
CrossTable(x=water$residence_area, y=water$africa)
#'
#'
#' Each cell in the table contains five numbers. The first one N give us the count that falls into its corresponding category. The Chi-square contribution provide us information about the cell's contribution in the Pearson's Chi-squared test for independence between two variables. This number measures the probability that the differences in cell counts are due to chance alone.
#'
#' The number of most interest is the `N/ Col Total` or the counts over column total. In this case, these numbers represent the distribution for residence area type among African regions and the regions in the rest of the world. We can see the numbers are very close between African and non-African regions for each type of residence area. Therefore, we can conclude that African WHO regions do not have a difference in terms of residence area types compared to the rest of the world.
#'
#' # Missing Data
#'
#' In the previous sections, we simply ignored the incomplete observations in our water dataset (`na.rm = TRUE`). Is this an appropriate strategy to handle incomplete data? Could the missingness pattern of those incomplete observations be important? It is possible that the arrangement of the missing observations may reflect an important factor that was not accounted for in our statistics or our models.
#'
#' **Missing Completely at Random (MCAR)** is an assumption about the probability of missingness being equal for all cases; **Missing at Random (MAR)** assumes the probability of missingness has a known but random mechanism (e.g., different rates for different groups); **Missing not at Random (MNAR)** suggest a missingness mechanism linked to the values of predictors and/or response, e.g., some participants may drop out of a drug trial when they have side-effects.
#'
#' There are a number of strategies to impute missing data. The [expectation maximization (EM) algorithm provides one example for handling missing data](https://doi.org/10.1016/0167-9473(93)E0056-A). The [SOCR EM tutorial, activity, and documentations](http://wiki.stat.ucla.edu/socr/index.php/SOCR_EduMaterials_Activities_2D_PointSegmentation_EM_Mixture) provides the theory, applications and practice for effective (multidimensional) EM parameter estimation.
#'
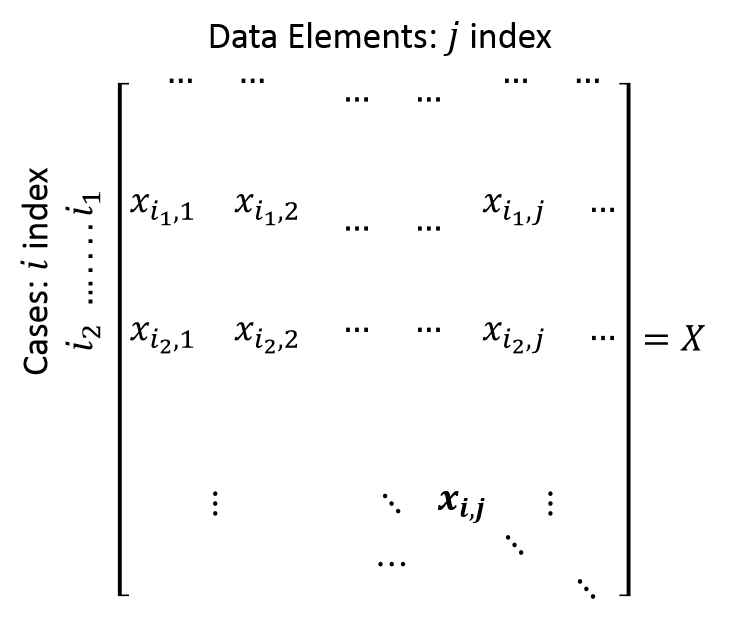
#' The simplest way to handle incomplete data is to substitute each missing value with its (feature or column) average. When the missingness proportion is small, the the effect of substituting the means for the missing values will have little effect on the mean, variance, or other important statistics of the data. Also, this will preserve those non-missing values of the same observation or row.
#'
#' 
#'
#'
m1<-mean(water$improved_water, na.rm = T)
m2<-mean(water$sanitation_facilities, na.rm = T)
water_imp<-water
for(i in 1:3331){
if(is.na(water_imp$improved_water[i])){
water_imp$improved_water[i]=m1
}
if(is.na(water_imp$sanitation_facilities[i])){
water_imp$sanitation_facilities[i]=m2
}
}
summary(water_imp)
#'
#'
#' A more sophisticated way of resolving missing data is to use a model (e.g., linear regression) to predict the missing feature and impute its missing values. This is called the `predictive mean matching approach`. This method is good for data with multivariate normality. However, a disadvantage of it is that it can only predict one value at a time, which is very time consuming. Also, the multivariate normality assumption might not be satisfied and there may be important multivariate relations that are not accounted for. We are using the `mi` package for the predictive mean matching procedure.
#'
#' Let's install the `mi` package first.
#'
# install.packages("mi")
library(mi)
#'
#'
#' Then we need to get the missing information matrix. We are using the imputation method `pmm`(predictive mean matching approach) for both missing variables.
#'
#'
mdf<-missing_data.frame(water)
head(mdf)
show(mdf)
mdf<-change(mdf, y="improved_water", what = "imputation_method", to="pmm")
mdf<-change(mdf, y="sanitation_facilities", what = "imputation_method", to="pmm")
#'
#'
#' * *Notes*:
#' + Converting the input `data.frame` to a `missing_data.frame` allows us to include in the DF enhanced metadata about each variable, which is essential for the subsequent modeling, interpretation and imputation of the initial missing data.
#' + `show()` displays all missing variables and their class-labels (e.g., continuous), along with meta-data. The `missing_data.frame` constructor suggests the most appropriate classes for each missing variable, however, the user often needs to correct, modify or change these meta-data, using `change()`.
#' + Use the `change()` function to change/correct many meta-data in the constructed `missing_data.frame` object which are incorrect when using `show(mfd)`.
#' + To get a sense of the raw data, look at the `summary`, `image`, or `hist` of the missing_data.frame.
#' + The [mi vignettes](https://cran.r-project.org/web/packages/mi/vignettes/mi_vignette.pdf) provide many useful examples of handling missing data.
#'
#' We can perform the initial imputation. Here we imputed 3 times, which will create 3 different datasets with slightly different imputed values.
#'
#'
imputations<-mi(mdf, n.iter=10, n.chains=3, verbose=T)
#'
#'
#' Next, we need to extract several multiply imputed `data.frames` from `imputations` object. Finally, we can compare the summary stats between the original dataset and the imputed datasets.
#'
#'
library(mi)
data.frames <- complete(imputations, 3)
summary(water)
summary(data.frames[[1]])
mySummary <- lapply(data.frames, summary)
mySummary$`chain:1` # report just the summary of the first chain.
#'
#'
#' This is just a brief introduction for handling incomplete datasets. In later chapters, we will discuss more about missing data with different imputation methods and how to evaluate the complete imputed results.
#'
#' ## Simulate some real multivariate data
#'
#' Suppose we would like to generate a synthetic dataset:
#' $$sim\_data=\{y, x1, x2, x3, x4, x5, x6, x7, x8, x9, x10\}.$$
#'
#' Then, we can introduce a method that takes a dataset and a desired proportion of missingness and wipes out the same proportion of the data, i.e., introduces random patterns of missingness. Note that there are already `R` functions that automate the introduction of missingness, e.g., `missForest::prodNA()`, however writing such method from scratch is also useful.
#'
#'
set.seed(123)
# create MCAR missing-data generator
create.missing <- function (data, pct.mis = 10)
{
n <- nrow(data)
J <- ncol(data)
if (length(pct.mis) == 1) {
if(pct.mis>= 0 & pct.mis <=100) {
n.mis <- rep((n * (pct.mis/100)), J)
}
else {
warning("Percent missing values should be an integer between 0 and 100! Exiting"); break
}
}
else {
if (length(pct.mis) < J)
stop("The length of the missing-vector is not equal to the number of columns in the data! Exiting!")
n.mis <- n * (pct.mis/100)
}
for (i in 1:ncol(data)) {
if (n.mis[i] == 0) { # if column has no missing do nothing.
data[, i] <- data[, i]
}
else {
data[sample(1:n, n.mis[i], replace = FALSE), i] <- NA
# For each given column (i), sample the row indices (1:n),
# a number of indices to replace as "missing", n.mis[i], "NA",
# without replacement
}
}
return(as.data.frame(data))
}
#'
#'
#' Next, let's synthetically generate (simulate) $1,000$ cases including all 11 features in the data ($\{y, x1, x2, x3, x4, x5, x6, x7, x8, x9, x10\}$).
#'
#'
n <- 1000; u1 <- rbinom(n, 1, .5); v1 <- log(rnorm(n, 5, 1)); x1 <- u1*exp(v1)
u2 <- rbinom(n, 1, .5); v2 <- log(rnorm(n, 5, 1)); x2 <- u2*exp(v2)
x3 <- rbinom(n, 1, prob=0.45); x4 <- ordered(rep(seq(1, 5), n)[sample(1:n, n)]); x5 <- rep(letters[1:10], n)[sample(1:n, n)]; x6 <- trunc(runif(n, 1, 10)); x7 <- rnorm(n); x8 <- factor(rep(seq(1, 10), n)[sample(1:n, n)]); x9 <- runif(n, 0.1, .99); x10 <- rpois(n, 4); y <- x1 + x2 + x7 + x9 + rnorm(n)
# package the simulated data as a data frame object
sim_data <- cbind.data.frame(y, x1, x2, x3, x4, x5, x6, x7, x8, x9, x10)
# randomly create missing values
sim_data_30pct_missing <- create.missing(sim_data, pct.mis=30);
# head(sim_data_30pct_missing); summary(sim_data_30pct_missing)
# install.packages("DT")
library("DT")
datatable(sim_data)
datatable(sim_data_30pct_missing)
# install.packages("mi")
# install.packages("betareg")
library("betareg"); library("mi")
# get show the missing information matrix
mdf <- missing_data.frame(sim_data_30pct_missing)
# show(mdf)
datatable(mdf)
# mdf@patterns # to get the textual missing pattern
image(mdf) # remember the visual pattern of this MCAR
#'
#'
#' In the missing data plot above, missing values are illustrated as `black` segments in the case-by-feature bivariate chart. The `hot` colormap (17-level) represents the *normalized* values of the corresponding feature-index pairs, see the [mi::image() documentation](https://github.com/cran/mi/blob/master/R/plot_methods.R). Also, test the `order`, `cluster` and `grayscale` options, e.g., `image(mdf, x.order = T, clustered = F, grayscale =T)`.
#'
#' The histogram plots display the distributions of:
#'
#' * The observed data (in blue color),
#' * The imputed data (in red color), and
#' * The completed values (observed plus imputed, in gray color).
#'
#'
# Next try to impute the missing values.
# Get the Graph Parameters (plotting canvas/margins)
# set to plot the histograms for the 3 imputation chains
# mfcol=c(nr, nc). Subsequent histograms are drawn as nr-by-nc arrays on the graphics device by columns (mfcol), or rows (mfrow)
# oma
# oma=c(bottom, left, top, right) giving the size of the outer margins in lines of text
# mar=c(bottom, left, top, right) gives the number of lines of margin to be specified on the four sides of the plot.
# tcl=length of tick marks as a fraction of the height of a line of text (default=0.5)
par(mfcol=c(5, 5), oma=c(1, 1, 0, 0), mar=c(1, 1, 1, 0), tcl=-0.1, mgp=c(0, 0, 0))
# Note to get verbose output-report, parallel must be OFF: parallel=FALSE, verbose=TRUE
imputations <- mi(sim_data_30pct_missing, n.iter=5, n.chains=3, verbose=TRUE)
hist(imputations)
# Extracts several multiply imputed data.frames from "imputations" object
data.frames <- complete(imputations, 3)
# compare the 3 objects, sim_data, sim_data_30pct_missing, and imputed chain1
datatable(sim_data, caption = htmltools::tags$caption(
style = 'caption-side: bottom; text-align: center;','Table: Initial sim_data'))
datatable(sim_data_30pct_missing, caption = htmltools::tags$caption(
style = 'caption-side: bottom; text-align: center;',
'Table: sim_data_30pct_missing'))
datatable(data.frames[[1]], caption = htmltools::tags$caption(
style = 'caption-side: bottom; text-align: center;',
'Table: Imputed data (chain 1)'))
# Compare the summary stats for the original data (prior to introducing missing
# values) with missing data and the re-completed data following imputation
# summary(sim_data)
datatable(data.frame(t(as.matrix(unclass(summary(sim_data)))), check.names = FALSE, stringsAsFactors = FALSE), caption = htmltools::tags$caption(
style = 'caption-side: bottom; text-align: center;',
'Table: summary(sim_data)'))
mySummary <- lapply(data.frames, summary)
datatable(data.frame(t(as.matrix(unclass(mySummary$`chain:1`))), check.names = FALSE, stringsAsFactors = FALSE), caption = htmltools::tags$caption(
style = 'caption-side: bottom; text-align: center;',
'Table: Imputed data: summary(chain:1)'))
#'
#'
#' Let's check imputation convergence (details provided below).
#'
#'
round(mipply(imputations, mean, to.matrix = TRUE), 3)
Rhats(imputations, statistic = "moments") # assess the convergence of MI algorithm
plot(imputations); hist(imputations); image(imputations); summary(imputations)
#'
#'
#' Finally, pool over the $m = 3$ completed datasets when we fit the "model".
#' Pool from across the 3 chains - in order to estimate a linear regression model.
#'
#'
model_results <- pool(y ~ x1+x2+x3+x4+x5+x6+x7+x8+x9+x10, data=imputations, m=3)
display (model_results); summary (model_results)
# Report the summaries of the imputations
data.frames <- complete(imputations, 3) # extract the first 3 chains
mySummary <-lapply(data.frames, summary)
datatable(data.frame(t(as.matrix(unclass(mySummary$`chain:1`))), check.names = FALSE, stringsAsFactors = FALSE), caption = htmltools::tags$caption(
style = 'caption-side: bottom; text-align: center;',
'Table: Imputed data: summary(chain:1)'))
datatable(data.frame(t(as.matrix(unclass(mySummary$`chain:2`))), check.names = FALSE, stringsAsFactors = FALSE), caption = htmltools::tags$caption(
style = 'caption-side: bottom; text-align: center;',
'Table: Imputed data: summary(chain:2)'))
datatable(data.frame(t(as.matrix(unclass(mySummary$`chain:3`))), check.names = FALSE, stringsAsFactors = FALSE), caption = htmltools::tags$caption(
style = 'caption-side: bottom; text-align: center;',
'Table: Imputed data: summary(chain:3)'))
coef(summary(model_results))[, 1:2] # get the model coef's and their SE's
library("lattice")
densityplot(y ~ x1 + x2, data=imputations)
# plot_ly(imputations@data$`chain:1`, x=~(x1+x2), y=~density(y))
# To compare the density of observed data and imputed data --
# these should be similar (though not identical) under MAR assumption
#'
#'
#'
#' **Notes**:
#'
#' * In general, it is recommended to generate multiple imputation chains and then analyze the data (e.g., estimate the model coefficients, obtain inference, compute likelihoods, etc.). *Pooling* the analytics across all chains accounts for between-chain as well as within-chain variability, [Rubin's rule](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2727536/).
#' * When deciding on how many chains to compute, a general rule is to compute $m$ chains if the rate of incomplete cases in the dataset is about $m \%$, i.e., 10-chains when 10% of cases are incomplete, [White et al.,2011](https://www.jstatsoft.org/article/view/v045i04/v45i04.pdf).
#' * For categorical features, e.g., binary predictors like $x_3$, the *display()* and *summary()* functions will report coefficient estimates for each (category) level, relative to the base level.
#'
#' ## TBI Data Example
#' Next, we will see an example using [the traumatic brain injury (TBI) dataset](https://wiki.socr.umich.edu/index.php/SMHS_MissingData#Raw_TBI_data). More information about the [clinical assesment scores (e.g., EGOS, GCS) is available in this publication (DOI: 10.1080/02699050701727460)](https://doi.org/10.1080/02699050701727460).
#'
#'
# Load the (raw) data from the table into a plain text file "08_EpiBioSData_Incomplete.csv"
TBI_Data <- read.csv("https://umich.instructure.com/files/720782/download?download_frd=1", na.strings=c("", ".", "NA")) ## 1. read in data
summary(TBI_Data)
# Get information matrix of the data
# 2. create an object of class "missing_data.frame" from the data.frame TBI_data
# Convert to a missing_data.frame
# library("betareg"); library("mi")
mdf <- missing_data.frame(TBI_Data) # warnings about missingness patterns
datatable(mdf); mdf@patterns; image(mdf)
# 3. get description of the "family", "imputation_method", "size", "transformation", "type", "link", or "model" of each incomplete variable
# show(mdf)
# 4. change things: mi::change() method changes the family, imputation method,
# size, type, and so forth of a missing variable. It's called
# before calling mi to affect how the conditional expectation of each
# missing variable is modeled.
mdf <- change(mdf, y = "spikes.hr", what = "transformation", to = "identity")
# The "to" choices include "identity" = no transformation, "standardize" = standardization, "log" = natural logarithm transformation, "logshift" = log(y + a) transformation, where a is a small constant, or "sqrt" = square-root variable transformation. Changing the transformation will correspondingly change the inverse transformation.
#'
#'
#'
# 5. examine missingness patterns
summary(mdf); hist(mdf);
image(mdf)
# 6. Perform initial imputation
imputations1 <- mi(mdf, n.iter=10, n.chains=5, verbose=TRUE)
hist(imputations1)
# 7. Extracts several multiply imputed data.frames from "imputations" object
data.frames1 <- complete(imputations1, 5)
# 8. Report a list of "summaries" for each element (imputation instance)
mySummary1 <- lapply(data.frames1, summary)
datatable(data.frame(t(as.matrix(unclass(mySummary1$`chain:1`))), check.names = FALSE, stringsAsFactors = FALSE), caption = htmltools::tags$caption(
style = 'caption-side: bottom; text-align: center;',
'Table: Imputed data: summary(chain:1)'),
extensions = 'Buttons', options = list(dom = 'Bfrtip',
buttons = c('copy', 'csv', 'excel', 'pdf', 'print')))
datatable(data.frame(t(as.matrix(unclass(mySummary1$`chain:5`))), check.names = FALSE, stringsAsFactors = FALSE), caption = htmltools::tags$caption(
style = 'caption-side: bottom; text-align: center;',
'Table: Imputed data: summary(chain:5)'),
extensions = 'Buttons', options = list(dom = 'Bfrtip',
buttons = c('copy', 'csv', 'excel', 'pdf', 'print')))
# 8.a. To cast the imputed numbers as integers (not necessary, but may be useful)
indx <- sapply(data.frames1[[5]], is.numeric) # get the indices of numeric columns
data.frames1[[5]][indx] <- lapply(data.frames1[[5]][indx], function(x) as.numeric(as.integer(x))) # cast each value as integer
# data.frames[[5]]$spikes.hr
# 9. Save results out
write.csv(data.frames1[[5]], "C:\\Users\\Dinov\\Desktop\\TBI_MIData.csv")
# 10. Complete Data analytics functions:
# library("mi")
#lm.mi(); glm.mi(); polr.mi(); bayesglm.mi(); bayespolr.mi(); lmer.mi(); glmer.mi()
# 10.1 Define Linear Regression for multiply imputed dataset - Also see Step (12)
##linear regression for each imputed data set - 5 regression models are fit
fit_lm1 <- glm(ever.sz ~ surgery + worst.gcs + factor(sex) + age, data.frames1$`chain:1`, family = "binomial"); summary(fit_lm1); display(fit_lm1)
# Fit the appropriate model and pool the results (estimates over MI chains)
model_results <- pool(ever.sz ~ surgery + worst.gcs + factor(sex) + age, family = "binomial", data=imputations1, m=5)
display (model_results); summary (model_results)
# Report the summaries of the imputations
data.frames <- complete(imputations1, 3) # extract the first 3 chains
mySummary2 <-lapply(data.frames1, summary)
datatable(data.frame(t(as.matrix(unclass(mySummary2$`chain:1`))), check.names = FALSE, stringsAsFactors = FALSE), caption = htmltools::tags$caption(
style = 'caption-side: bottom; text-align: center;',
'Table: Imputed data: summary(chain:1)'))
# 11. Validation: we now verify whether enough iterations were conducted.
# Validation criteria demands that the mean of each completed variable should
# be similar for each of the k chains (in this case k=5).
# mipply is wrapper for sapply invoked on mi-class objects to compute the col means
round(mipply(imputations1, mean, to.matrix = TRUE), 3)
# Rhat convergence statistics compares the variance between chains to the variance
# within chains (similar to the ANOVA F-test).
# Rhat Values ~ 1.0 indicate likely convergence,
# Rhat Values > 1.1 indicate that the chains should be run longer
# (use large number of iterations)
Rhats(imputations1, statistic = "moments") # assess the convergence of MI algorithm
# When convergence is unstable, we can continue the iterations for all chains, e.g.
imputations1 <- mi(imputations1, n.iter=20) # add additional 20 iterations
# To plot the produced mi results, for all missing_variables we can generate
# a histogram of the observed, imputed, and completed data.
# We can compare of the completed data to the fitted values implied by the model
# for the completed data, by plotting binned residuals.
# hist function works similarly as plot.
# image function gives a sense of the missingness patterns in the data
plot(imputations1); hist(imputations1); image(imputations1)
mySummary3 <-lapply(data.frames1, summary)
datatable(data.frame(t(as.matrix(unclass(mySummary3$`chain:1`))), check.names = FALSE, stringsAsFactors = FALSE), caption = htmltools::tags$caption(
style = 'caption-side: bottom; text-align: center;',
'Table: Imputed data: summary(chain:1)'))
# 12. Finally, pool over the m = 5 imputed datasets when we fit the "model"
# Pool from across the 4 chains - in order to estimate a linear regression model
# and impact of various predictors
model_results <- pool(ever.sz ~ surgery + worst.gcs + factor(sex) + age, data = imputations1, m = 5 ); display (model_results); summary (model_results)
coef(summary(model_results))[, 1:2] # get the model coef's and their SE's
#'
#'
#' ## Imputation via Expectation-Maximization
#'
#' Below we present the theory and practice of one specific statistical computing strategy for imputing incomplete datasets.
#'
#' ### Types of missing data
#'
#' * **MCAR**: Data which is Missing Completely At Random has nothing systematic about which observations are missing. There is no relationship between missingness and either observed or unobserved covariates.
#'
#' * **MAR**: Missing At Random is weaker than MCAR. The missingness is still random, but solely due to the observed variables. For example, those from a lower socioeconomic status (SES) may be less willing to provide salary information (but we know their SES). The key is that the missingness is not due to the values which are not observed. MCAR implies MAR, but not vice-versa.
#'
#' * **MNAR**: If the data are Missing Not At Random, then the missingness depends on the values of the missing data. Examples include censored data, self-reported data for individuals who are heavier, who are less likely to report their weight, and response-measuring device that can only measure values above $0.5$, anything below that is missing.
#'
#' ### General Idea of EM algorithm
#'
#' [Expectation-Maximization (EM) is an iterative process](http://repositories.cdlib.org/socr/EM_MM) involving two steps - *expectation* and *maximization*, which are applied in tandem. EM can be employed to find parameter estimates using maximum likelihood and is specifically useful when the equations determining the relations of the data-parameters cannot be directly solved. For example, a Gaussian mixture modeling assumes that each data point ($X$) has a corresponding latent (unobserved) variable or a missing value ($Y$), which may be specified as a mixture of coefficients determining the affinity of the data as a linear combination of Gaussian kernels, determined by a set of parameters ($\theta$), e.g., means and variance-covariances. Thus, EM estimation relies on:
#'
#' * An observed data set $X$,
#' * A set of missing (or latent) values $Y$,
#' * A parameter $\theta$, which may be a vector of parameters,
#' * A likelihood function $L(\theta | X, Y) =p(X,Y |\theta)$, and
#' * The maximum likelihood estimate (MLE) of the unknown parameter(s) $\theta$ that is computed using the marginal likelihood of the observed data:
#'
#' $$L(\theta | X) = p(X |\theta) =\int { p(X, Y |\theta)dY}.$$
#'
#' Most of the time, this equation may not be directly solved, e.g., when $Y$ is missing.
#'
#' * *Expectation step (E step)*: computes the expected value of the *log likelihood function*, with respect to the conditional distribution of $Y$ given $X$ using the parameter estimates at the previous iteration (or at the position of initialization, for the first iteration), $\theta_t$:
#'
#' $$Q ( \theta | \theta^{(t)} ) = E_{Y | X, \theta^{(t)} }[ log
#' \left ( L(\theta | X , Y ) \right ];$$
#'
#' * *Maximization step (M step)*: Determine the parameter, $\theta$, that maximizes the expectation above, $$\theta^{(t+1)}=\arg\max_{\theta}Q(\theta|\theta^{(t)}).$$
#'
#' [This SOCR EM Activity](http://wiki.stat.ucla.edu/socr/index.php/SOCR_EduMaterials_Activities_2D_PointSegmentation_EM_Mixture) shows the practical aspects of applying the EM algorithm. Also, in [DSPA Chapter 3](https://www.socr.umich.edu/people/dinov/courses/DSPA_notes/03_DataVisualization.html#61_data_modeler) we will illustrate the EM method for fitting single *distribution models* or (linear) *mixtures of distributions* to data that may represent a blend of heterogeneous observations from multiple different processes.
#'
#' ### EM-based imputation
#' The EM algorithm is an alternative to Newton-Raphson or the method of scoring for computing MLE in cases where there are complications in calculating the MLE. It is applicable for imputing incomplete MAR data, where the missing data mechanism can be ignored and separate parameters may be estimated for each missing feature.
#'
#' **Complete Data: **
#' $$
#' Z =
#' \left(\begin{array}{cc}
#' X \\
#' Y
#' \end{array}\right),
#' ZZ^T = \left(\begin{array}{cc}
#' XX^T & XY^T \\
#' YX^T & YY^T
#' \end{array}\right),
#' $$
#'
#' where $X$ is the observed data and $Y$ is the missing data.
#'
#' * E-step: (Expectation) Get the expectations of $Y$ and $YY^T$ based on observed data, $X$.
#' * M-step: (Maximization) Maximize the conditional expectation in E-step to estimate the parameters.
#'
#' **Details:** If $o=obs$ and $m=mis$ stand for observed and missing, the mean vector, $(\mu_{obs}, \mu_{mis})^T$, and the variance-covariance matrix, $\Sigma^{(t)} = \left(\begin{array}{cc} \Sigma_{oo} & \Sigma_{om} \\ \Sigma_{mo} & \Sigma_{mm} \end{array}\right)$, are represented by:
#'
#' $$
#' \mu^{(t)} =
#' \left(\begin{array}{cc}
#' \mu_{obs} \\
#' \mu_{mis}
#' \end{array}\right),\;\;\;\;\;
#' \Sigma^{(t)} = \left(\begin{array}{cc}
#' \Sigma_{oo} & \Sigma_{om} \\
#' \Sigma_{mo} & \Sigma_{mm}
#' \end{array}\right)
#' $$
#' **E-step:**
#' $$
#' E(Z | X) =
#' \left(\begin{array}{cc}
#' X \\
#' E(Y|X)
#' \end{array}\right),\;\;\;\;\;
#' E(ZZ^T|X) = \left(\begin{array}{cc}
#' XX^T & XE(Y|X)^T \\
#' E(Y|X)X^T & E(YY^T|X)
#' \end{array}\right).
#' $$
#'
#' $$E(Y | X) = \mu_{mis} + \Sigma_{mo}\Sigma_{oo}^{-1}(X - \mu_{obs}).$$
#' $$E(YY^T|X) = (\Sigma_{mm}-\Sigma_{mo}\Sigma_{oo}^{-1}\Sigma_{om})+E(Y|X)E(Y|X)^T.$$
#'
#' **M-step:**
#' $$\mu^{(t+1)} = \frac{1}{n}\sum_{i=1}^nE(Z|X).$$
#' $$\Sigma^{(t+1)} = \frac{1}{n}\sum_{i=1}^nE(ZZ^T|X) - \mu^{(t+1)}{\mu^{(t+1)}}^T.$$
#'
#' ### A simple manual implementation of EM-based imputation
#'
#'
# install.packages(c("gridExtra", "MASS"))
require(ggplot2)
require(gridExtra)
require(MASS)
require(knitr)
#'
#'
#'
# simulate 20 (feature) vectors of 200 (cases) Normal Distributed random values (\mu, \Sigma)
# You can choose multiple distribution for testing
# sim_data <- replicate(20, rpois(50, 10))
set.seed(202227)
mu <- as.matrix(rep(2,20) )
sig <- diag(c(1:20) )
# Add a noise item. The noise is $ \epsilon ~ MVN(as.matrix(rep(0,20)), diag(rep(1,20)))$
sim_data <- mvrnorm(n = 200, mu, sig) +
mvrnorm(n=200, as.matrix(rep(0,20)), diag( rep(1,20) ))
# save these in the "original" object
sim_data.orig <- sim_data
# install.packages("e1071")
# introduce 500 random missing indices (in the total of 4000=200*20)
# discrete distribution where the probability of the elements of values is proportional to probs,
# which are normalized to add up to 1.
rand.miss <- e1071::rdiscrete(500, probs = rep(1,length(sim_data)), values = seq(1, length(sim_data)))
sim_data[rand.miss] <- NA
sum(is.na(sim_data)) # check now many missing (NA) are there < 500
# cast the data into a data.frame object and report 15*10 elements
sim_data.df <- data.frame(sim_data)
# kable( sim_data.df[1:15, 1:10], caption = "The first 15 rows and first 10 columns of the simulation data")
datatable(sim_data.df, caption = htmltools::tags$caption(
style = 'caption-side: bottom; text-align: center;',
'Table: Simulated Data (sim_data.df)'),
extensions = 'Buttons', options = list(dom = 'Bfrtip',
buttons = c('copy', 'csv', 'excel', 'pdf', 'print')))
# Define the EM imputation method
EM_algorithm <- function(x, tol = 0.001) {
# identify the missing data entries (Boolean indices)
missvals <- is.na(x)
# instantiate the EM-iteration
new.impute <- x
old.impute <- x
count.iter <- 1
reach.tol <- 0
# compute \Sigma on complete data
sigma <- as.matrix(var(na.exclude(x)))
# compute the vector of feature (column) means
mean.vec <- as.matrix(apply(na.exclude(x), 2, mean))
while (reach.tol != 1) {
for (i in 1:nrow(x)) {
pick.miss <- (c(missvals[i, ]))
if (sum(pick.miss) != 0) {
# compute inverse-Sigma_completeData, variance-covariance matrix
inv.S <- solve(sigma[!pick.miss, !pick.miss], tol = 1e-40)
# Expectation Step
# $$E(Y|X)=\mu_{mis}+\Sigma_{mo}\Sigma_{oo}^{-1}(X-\mu_{obs})$$
new.impute[i, pick.miss] <- mean.vec[pick.miss] +
sigma[pick.miss,!pick.miss] %*% inv.S %*%
(t(new.impute[i, !pick.miss]) - t(t(mean.vec[!pick.miss])))
}
}
# Maximization Step
# Recompute the complete \Sigma the complete vector of feature (column) means
#$$\Sigma^{(t+1)} = \frac{1}{n}\sum_{i=1}^nE(ZZ^T|X) - \mu^{(t+1)}{\mu^{(t+1)}}^T$$
sigma <- var((new.impute))
#$$\mu^{(t+1)} = \frac{1}{n}\sum_{i=1}^nE(Z|X)$$
mean.vec <- as.matrix(apply(new.impute, 2, mean))
# Inspect for convergence tolerance, start with the 2nd iteration
if (count.iter > 1) {
for (l in 1:nrow(new.impute)) {
for (m in 1:ncol(new.impute)) {
if (abs((old.impute[l, m] - new.impute[l, m])) > tol) {
reach.tol <- 0
} else {
reach.tol <- 1
}
}
}
}
count.iter <- count.iter + 1
old.impute <- new.impute
}
# return the imputation output of the current iteration that passed the tolerance level
return(new.impute)
}
sim_data.imputed <- EM_algorithm(sim_data.df, tol=0.0001)
#'
#'
#' ### Plotting complete and imputed data
#'
#' Smaller black colored points represent observed data, and magenta-color and circle-shapes denote the imputed data.
#'
#'
plot.me <- function(index1, index2){
plot.imputed <- sim_data.imputed[row.names(
subset(sim_data.df, is.na(sim_data.df[, index1]) | is.na(sim_data.df[, index2]))), ]
p = ggplot(sim_data.imputed, aes_string( paste0("X",index1) , paste0("X",index2 ))) +
geom_point(alpha = 0.5, size = 0.7)+theme_bw() +
stat_ellipse(type = "norm", color = "#000099", alpha=0.5) +
geom_point(data = plot.imputed, aes_string( paste0("X",index1) , paste0("X",(index2))),size = 1.5, color = "Magenta", alpha = 0.8)
}
gridExtra::grid.arrange( plot.me(1,2), plot.me(5,6), plot.me(13,20), plot.me(18,19), nrow = 2)
index1=1; index2=5
plot.imputed <- sim_data.imputed[row.names(
subset(sim_data.df, is.na(sim_data.df[, index1]) | is.na(sim_data.df[, index2]))), ]
p = ggplot(sim_data.imputed, aes_string( paste0("X",index1) , paste0("X",index2 ))) +
geom_point(alpha = 0.5, size = 0.7)+theme_bw() +
stat_ellipse(type = "norm", color = "#000099", alpha=0.5) +
geom_point(data = plot.imputed, aes_string( paste0("X",index1) , paste0("X",(index2))),size = 1.5, color = "Magenta", alpha = 0.8)
plot_ly(sim_data.imputed, x = ~X1, y = ~X5, type = "scatter",
mode = "markers") %>%
layout(title='Scatterplot: Improved Water Quality vs. Sanitation Facilities',
xaxis = list (title = 'Water Quality'), yaxis = list (title = 'Sanitation'))
#'
#'
#' ### Validation of EM-imputation using the `Amelia` R Package
#'
#' * [Paper](https://gking.harvard.edu/files/gking/files/amelia_jss.pdf),
#' * [R manual](https://cran.r-project.org/web/packages/Amelia/Amelia.pdf).
#'
#'
# knitr::include_graphics("ammelia.png")
#'
#'
#' #### Comparison
#'
#' Let's use the `amelia` function to impute the original data *sim_data_df* and compare the results to the simpler manual `EM_algorithm` imputation defined above.
#'
#'
# install.packages("Amelia")
library(Amelia)
dim(sim_data.df)
amelia.out <- amelia(sim_data.df, m = 5)
amelia.out
amelia.imputed.5 <- amelia.out$imputations[[5]]
#'
#'
#' * **Magenta-color and circle-shape denote manual imputation via `EM_algorithm`**
#' * **Orange-color and square-shapes denote Amelia imputation**
#'
#'
plot.ii2 <- function(index, index2){
plot.imputed <- sim_data.imputed[row.names(
subset(sim_data.df, is.na(sim_data.df[, index]) | is.na(sim_data.df[, index2]))), ]
plot.imputed2 <- amelia.imputed.5[row.names(
subset(sim_data.df, is.na(sim_data.df[, index]) | is.na(sim_data.df[, index2]))), ]
p = ggplot(sim_data.imputed, aes_string( paste0("X",index) , paste0("X",index2 ))) +
geom_point(alpha = 0.8, size = 0.7)+theme_bw() +
stat_ellipse(type = "norm", color = "#000099", alpha=0.5) +
geom_point(data = plot.imputed, aes_string( paste0("X",index) , paste0("X",(index2))),size = 2.5, color = "Magenta", alpha = 0.9, shape = 16) +
geom_point(data = plot.imputed2, aes( X1 , X2),size = 2.5, color = "#FF9933", alpha = 0.8, shape = 18)
return(p)
}
plot.ii2(2, 4)
plot.ii2(17, 18)
#'
#'
#' #### Density plots
#'
#' Finally, we can compare the densities of the original, manually-imputed and Amelia-imputed datasets. Remember that in this simulation, we had about $500$ observations missing out of the $4,000$ that we synthetically generated.
#'
#'
# plot.ii3 <- function(index){
# imputed <- sim_data.imputed[is.na(sim_data.df[, index]) , index]
# imputed.amelia <- amelia.imputed.5[is.na(sim_data.df[, index]) , index]
# observed <- sim_data.df[!is.na(sim_data.df[, index]) , index]
# imputed.df <- data.frame(x = c(observed,imputed,imputed.amelia), category = c( rep("obs",length(observed)),rep("simpleImplement",length(imputed)) ,rep("amelia",length(imputed.amelia)) ) )
# p = ggplot(imputed.df, aes(x=x, y =..density..)) +
# geom_density(aes(fill = category),alpha=0.3)+
# theme_bw()
# return(p)
# }
# grid.arrange( plot.ii3(1),plot.ii3(2),plot.ii3(3),plot.ii3(4),plot.ii3(5),
# plot.ii3(6),plot.ii3(7),plot.ii3(8),plot.ii3(9),plot.ii3(10),
# nrow = 5)
library(tidyr)
myPlotly <- function(index){
imputed <- sim_data.imputed[is.na(sim_data.df[, index]) , index]
imputed.amelia <- amelia.imputed.5[is.na(sim_data.df[, index]) , index]
observed <- sim_data.df[!is.na(sim_data.df[, index]) , index]
imputed.df <- data.frame(x = c(observed,imputed,imputed.amelia),
category = c( rep("obs",length(observed)),rep("simpleImplement",length(imputed)),
rep("amelia",length(imputed.amelia)) ) )
df_long <- as.data.frame(cbind(index=c(1:length(imputed.df$x)),
category=imputed.df$category, x=imputed.df$x))
df_wide <- spread(df_long, category, x)
p = plot_ly() %>%
add_lines(x = ~density(as.numeric(df_wide$simpleImplement), na.rm = T)$x,
y= ~density(as.numeric(df_wide$simpleImplement), na.rm = T)$y, name = "EM", mode = 'lines') %>%
add_lines(x = density(as.numeric(df_wide$amelia), na.rm = T)$x,
y= density(as.numeric(df_wide$amelia), na.rm = T)$y, name = "Amelia", mode = 'lines') %>%
add_lines(x = ~density(as.numeric(df_wide$obs), na.rm = T)$x,
y= ~density(as.numeric(df_wide$obs), na.rm = T)$y, name = "Observed", mode = 'lines') %>%
layout(title=sprintf("Distributions: Feature X.%d", index),
xaxis = list(title = 'Measurements'),
yaxis = list(title ="Densities"),
legend = list(title="Distributions", orientation = 'h'))
return(p)
}
# Plot a few features
myPlotly(5)
myPlotly(9)
myPlotly(10)
# grid.arrange( myPlotly(1),myPlotly(2),myPlotly(3),myPlotly(4),myPlotly(5),
# myPlotly(6),myPlotly(7),myPlotly(8),myPlotly(9),myPlotly(10),
# nrow = 5)
#'
#'
#' # Parsing webpages and visualizing tabular HTML data
#'
#' In this section, we will utilize the Earthquakes dataset on [SOCR website](https://wiki.socr.umich.edu/index.php/SOCR_Data_Dinov_021708_Earthquakes). It records information about earthquakes happened between 1969 and 2007 with magnitudes larger than 5 on the Richter scale. Here is how we parse the data on the source webpage and ingest the information into R:
#'
#'
# install.packages("xml2")
library("XML"); library("xml2")
library("rvest")
wiki_url <- read_html("https://wiki.socr.umich.edu/index.php/SOCR_Data_Dinov_021708_Earthquakes")
html_nodes(wiki_url, "#content")
earthquake<- html_table(html_nodes(wiki_url, "table")[[2]])
#'
#'
#' In this dataset, `Magt`(magnitude type) may be used as grouping variable. We will draw a "Longitude vs Latitude" line plot from this dataset. The function we are using is called `ggplot()` under `ggplot2`. The input type for this function is mostly data frame. `aes()` specifies axes.
#'
#'
# library(ggplot2)
# plot4<-ggplot(earthquake, aes(Longitude, Latitude, group=Magt, color=Magt))+
# geom_point(data=earthquake, size=4, mapping=aes(x=Longitude, y=Latitude, shape=Magt))
# plot4 # or plint(plot4)
# https://plotly-r.com/working-with-symbols.html
glyphication <- function (name) {
glyph= vector()
for (i in 1:length(name)){
glyph[i]="triangle-up"
if (name[i]=="Md") { glyph[i]="diamond-open" }
else if (name[i]=="ML") { glyph[i]="circle-open" }
else if (name[i]=="Mw") { glyph[i]="square-open" }
else if (name[i]=="Mx") { glyph[i]="x-open" }
}
return(glyph)
}
earthquake$glyph <- glyphication(earthquake$Magt)
plot_ly(earthquake) %>%
add_markers(x = ~Longitude, y = ~Latitude, type = "scatter", color = ~Magt,
mode = "markers", marker = list(size = ~Depth, color = ~Magt, symbol = ~glyph,
line = list(color = "black",width = 2))) %>%
layout(title="California Earthquakes (1969 - 2007)")
#'
#'
#' We can see the most important line of code was made up with 2 parts. The first part `ggplot(earthquake, aes(Longiture, Latitude, group=Magt, color=Magt))` specifies the setting of the plot: dataset, group and color. The second part specifies we are going to draw lines between data points. In later chapters we will frequently use package `ggplot2` and the structure under this great package is always `function1+function2`.
#'
#' We can visualize the distribution for different variables using density plots. The following chunk of codes plots the distribution for Latitude among different Magnitude types. Also, it is using `ggplot()` function but combined with `geom_density()`.
#'
#'
plot5<-ggplot(earthquake, aes(Latitude, size=1))+geom_density(aes(color=Magt))
plot5
#'
#'
#' We can also compute and display 2D Kernel Density and 3D Surface Plots. Plotting 2D Kernel Density and 3D Surface plots is very important and useful in multivariate exploratory data analytic.
#'
#' We will use `plot_ly()` function under `plotly` package, which takes value from a data frame.
#'
#' To create a surface plot, we use two vectors: *x* and *y* with length *m* and *n* respectively. We also need a matrix: *z* of size $m\times n$. This *z* matrix is created from matrix multiplication between *x* and *y*.
#'
#' The `kde2d()` function is needed for 2D kernel density estimation.
#'
#'
kernal_density <- with(earthquake, MASS::kde2d(Longitude, Latitude, n = 50))
#'
#'
#' Here `z` is an estimate of the kernel density function. Then we apply `plot_ly` to the list `kernal_density` via `with()` function.
#'
#'
library(plotly)
with(kernal_density, plot_ly(x=x, y=y, z=z, type="surface"))
#'
#'
#' Note that we used the option `"surface"`, however you can experiment with the `type` option.
#'
#' Alternatively, one can plot 1D, 2D or 3D plots:
#'
#'
plot_ly(x = ~ earthquake$Longitude)
plot_ly(x = ~ earthquake$Longitude, y = ~earthquake$Latitude)
plot_ly(x = ~ earthquake$Longitude, y = ~earthquake$Latitude, z=~earthquake$Mag)
df3D <- data.frame(x=earthquake$Longitude, y=earthquake$Latitude, z=earthquake$Mag)
# Convert he Long (X, Y, Z) Earthquake format data into a Matrix Format
# install.packages("Matrix")
library("Matrix")
matrix_EarthQuakes <- with(df3D, sparseMatrix(i = as.numeric(180-x), j=as.numeric(y), x=z, use.last.ij=T, dimnames=list(levels(x), levels(y))))
dim(matrix_EarthQuakes)
# colnames(matrix_EarthQuakes) <- seq(from=earthquake$Longitude[1],
# to=earthquake$Longitude[length(earthquake$Longitude)],
# length.out=dim(matrix_EarthQuakes)[2])
# rownames(matrix_EarthQuakes) <- seq(from=earthquake$Latitude[1],
# to=earthquake$Latitude[length(earthquake$Latitude)],
# length.out=dim(matrix_EarthQuakes)[1])
# View(as.matrix(matrix_EarthQuakes))
# view matrix is 2D heatmap:
library("ggplot2"); library("gplots")
# heatmap.2( as.matrix(matrix_EarthQuakes[280:307, 30:44]), Rowv=FALSE, Colv=FALSE, dendrogram='none', cellnote=as.matrix(matrix_EarthQuakes[280:307, 30:44]), notecol="black", trace='none', key=FALSE, lwid = c(.01, .99), lhei = c(.01, .99), margins = c(5, 15 ))
plot_ly(z = ~as.matrix(matrix_EarthQuakes[280:307, 30:44]), type = "heatmap") %>% hide_colorbar()
# plot_ly(x=~colnames(matrix_EarthQuakes[280:307, 30:44]),
# y=~rownames(matrix_EarthQuakes[280:307, 30:44]),
# z = ~as.matrix(matrix_EarthQuakes[280:307, 30:44]), type = "heatmap") %>%
# layout(title="California Earthquakes Heatmap",
# xaxis=list(title="Longitude"), yaxis=list(title="Latitude")) %>%
# hide_colorbar()
# Long -180%
add_lines(x=c(0,0.8), y=c(0,0.8), showlegend=F) %>%
layout(title="QQ-Plot Original vs. Rebalanced Data", xaxis=list(title="original data"),
yaxis=list(title="Rebalanced data"))
###Check balance
## Wilcoxon test
alpha.0.05 <- 0.05
test.results.bin <- NULL # binarized/dichotomized p-values
test.results.raw <- NULL # raw p-values
for (i in 1:(ncol(balancedData)-1))
{
test.results.raw [i] <- wilcox.test(input[, i], balancedData [, i])$p.value
test.results.bin [i] <- ifelse(test.results.raw [i] > alpha.0.05, 1, 0)
print(c("i=", i, "Wilcoxon-test=", test.results.raw [i]))
}
print(c("Wilcoxon test results: ", test.results.bin))
test.results.corr <- stats::p.adjust(test.results.raw, method = "fdr", n = length(test.results.raw))
# where methods are "holm", "hochberg", "hommel", "bonferroni", "BH", "BY", "fdr", "none")
# plot(test.results.raw, test.results.corr)
# zeros (0) are significant independent between-group T-test differences, ones (1) are insignificant
plot_ly(x=~test.results.raw, y = ~test.results.corr, type="scatter", mode="markers", showlegend=F) %>%
add_lines(x=c(0,1), y=c(0,1), showlegend=F) %>%
layout(title="Wilcoxon test results - Original vs. Rebalanced Data", xaxis=list(title="Original"),
yaxis=list(title="Rebalanced"))
# Check the Differences between the rate of significance between the raw and FDR-corrected p-values
test.results.bin <- ifelse(test.results.raw > alpha.0.05, 1, 0)
table(test.results.bin)
test.results.corr.bin <- ifelse(test.results.corr > alpha.0.05, 1, 0)
table(test.results.corr.bin)
#'
#'
#' **Notes**
#'
#' * SMOTE over-sampling of the minority cohort is via generation of synthetic minority samples within the neighborhoods of observed observations. Thus, new minority instances
#' blend observations in the same class and create clusters around each observed minority element.
#' * The `percOver` parameter (perc.over/100) represents the number of new instances generated for each rare instance in the minority sample, when $perc.over < 100$, a single instance is generated. For example, `percOver=300` and `percOver=30` would triple (300/100) and leave unchanged (30/100) the size of the *minority sample*, respectively.
#' * The $k$ parameter represents the number of neighbors to consider as the aggregate pool that the new examples are generated.
#' * The `percUnder` (perc.under/100) represents the number of "normal" (majority class) instances that are randomly selected for each *smoted* (synthetically generated) observation. For instance, `percUnder=300` or `percUnder=30` would downsample the *majority sample* by choosing one-out-of-each-three or all of the majority sample points, respectively.
#'
#' # Appendix
#'
#' ## Importing Data from SQL Databases
#'
#' We can also import SQL databases in to R. First, we need to install and load the RODBC(R Open Database Connectivity) package.
#'
#'
# install.packages("RODBC", repos = "http://cran.us.r-project.org")
library(RODBC)
#'
#'
#' Then, we could open a connection to the SQL server database with Data Source Name (DSN), via Microsoft Access. More details are provided [here](https://technet.microsoft.com/en-us/library/cc879308%28v=sql.105%29.aspx) and [here](https://cran.r-project.org/web/packages/RODBC/vignettes/RODBC.pdf).
#'
#' ## R codes for graphs shown in this chapter
#'
#Right Skewed
N <- 10000
x <- rnbinom(N, 10, .5)
hist(x,
xlim=c(min(x), max(x)), probability=T, nclass=max(x)-min(x)+1,
col='lightblue', xlab=' ', ylab=' ', axes=F,
main='Right Skewed')
lines(density(x, bw=1), col='red', lwd=3)
#No Skew
N <- 10000
x <- rnorm(N, 0, 1)
hist(x, probability=T,
col='lightblue', xlab=' ', ylab=' ', axes=F,
main='No Skew')
lines(density(x, bw=0.4), col='red', lwd=3)
#Uniform density
x<-runif(1000, 1, 50)
hist(x, col='lightblue', main="Uniform Distribution", probability = T, xlab="", ylab="Density", axes=F)
abline(h=0.02, col='red', lwd=3)
#68-95-99.7 rule
x <- rnorm(N, 0, 1)
hist(x, probability=T,
col='lightblue', xlab=' ', ylab=' ', axes = F,
main='68-95-99.7 Rule')
lines(density(x, bw=0.4), col='red', lwd=3)
axis(1, at=c(-3, -2, -1, 0, 1, 2, 3), labels = expression(mu-3*sigma, mu-2*sigma, mu-sigma, mu, mu+sigma, mu+2*sigma, mu+3*sigma))
abline(v=-1, lwd=3, lty=2)
abline(v=1, lwd=3, lty=2)
abline(v=-2, lwd=3, lty=2)
abline(v=2, lwd=3, lty=2)
abline(v=-3, lwd=3, lty=2)
abline(v=3, lwd=3, lty=2)
text(0, 0.2, "68%")
segments(-1, 0.2, -0.3, 0.2, col = 'red', lwd=2)
segments(1, 0.2, 0.3, 0.2, col = 'red', lwd=2)
text(0, 0.15, "95%")
segments(-2, 0.15, -0.3, 0.15, col = 'red', lwd=2)
segments(2, 0.15, 0.3, 0.15, col = 'red', lwd=2)
text(0, 0.1, "99.7%")
segments(-3, 0.1, -0.3, 0.1, col = 'red', lwd=2)
segments(3, 0.1, 0.3, 0.1, col = 'red', lwd=2)
#'
#'
#'
#'